\(\displaystyle ABCD\) дөңес төртбұрышында \(\displaystyle DAC\) және \(\displaystyle DBC\) бұрыштары тең.
\(\displaystyle a) \) \(\displaystyle CDB\) және \(\displaystyle CAB\) бұрыштары да тең екенін дәлелдеңіз.
\(\displaystyle б)\) \(\displaystyle BAC \) бұрышының шамасын табыңыз, егер \(\displaystyle \angle CBD=67^{\circ}{\small,}\) \(\displaystyle \angle BCD=94^{\circ}{\small.}\) Жауабын градуспен беріңіз.
\(\displaystyle a) \) Есептің шарты бойынша сызбаны орындаймыз.
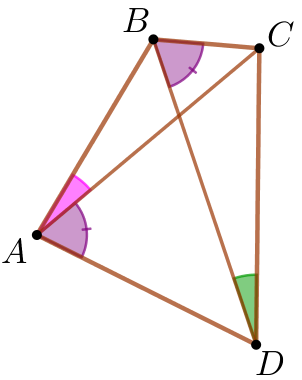 | \(\displaystyle ABCD\)– дөңес төртбұрыш. \(\displaystyle \angle DAC=\angle DBC{\small.}\)
\(\displaystyle CDB\) және \(\displaystyle CAB\) бұрыштары тең екенін дәлелдеу қажет. |
Кез келген үшбұрыштың айналасында шеңберді, және тек біреуін сызуға болады.
Сырттай сызылған шеңбердің радиусын синустар теоремасы арқылы табуға болады.
Синустар теоремасы
\(\displaystyle \frac{\color{Purple}{a}}{\sin(\angle A)}=\frac{\color{green}{b}}{\sin(\angle B)}=\frac{\color{blue}{c}}{\cos(\angle C)}=2\color{red}{R}{\small,}\) мұндағы \(\displaystyle \color{red}{R}\) – сырттай сызылған шеңбердің радиусы. |
\(\displaystyle ACD\) және \(\displaystyle BCD{\small}\) үшбұрыштарын қарастырайық
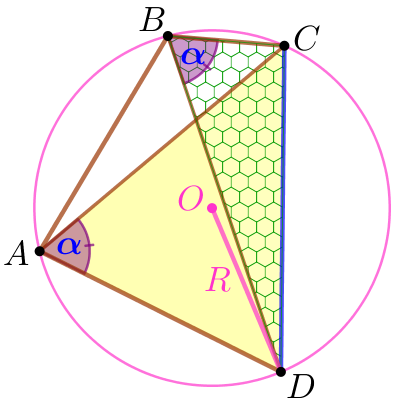 |
\(\displaystyle ACD{\small,}\) үшбұрышының сыртынан сызылған шеңбердің радиусы \(\displaystyle BCD\) үшбұрышының сыртынан сызылған шеңбердің радиусына тең және \(\displaystyle R=\frac{CD}{2 \cdot \sin\alpha} {\small.}\) |
Яғни, \(\displaystyle A{\small,}\,B{\small,}\,C{\small,}\,D\) нүктелері бір шеңберде жатыр.
\(\displaystyle ABCD\) төртбұрышы шеңбердің ішіне сызылғанын алдық.
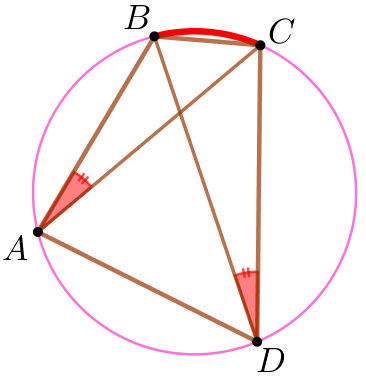 | Шеңберде бір доғаға тірелген іштей сызылған бұрыштар тең болады. \(\displaystyle CDB\) және \(\displaystyle CAB\) іштей салынған бұрыштар \(\displaystyle \overset{\smile}{BC} {\small}\) бір доғаға тіреледі. Яғни, \(\displaystyle \angle CDB=\angle CAB{\small.}\) |
Тұжырым дәлелденді.
\(\displaystyle б)\) Есептің шарты бойынша \(\displaystyle \angle CBD=67^{\circ}{\small,}\) \(\displaystyle \angle BCD=94^{\circ}{\small.}\)
\(\displaystyle BAC {\small}\) бұрышының шамасын табу қажет
\(\displaystyle a)\) тармағында дәлелденген бойынша \(\displaystyle \angle BAC=\angle CDB{\small.}\)
\(\displaystyle BCD{\small}\) үшбұрышын қарастырайық
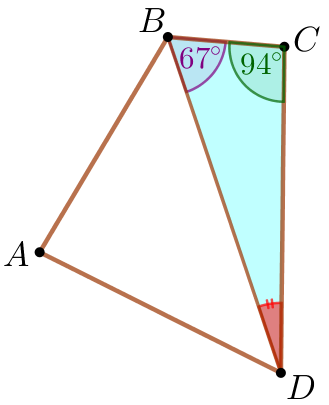 | Үшбұрыштың ішкі бұрыштарының қосындысы \(\displaystyle 180^{\circ} {\small}\) тең. \(\displaystyle \angle CDB+\angle BCD+\angle CBD=180^{\circ} {\small;}\) \(\displaystyle \angle CDB=180^{\circ}-(\angle BCD+\angle CBD) {\small;}\) \(\displaystyle \angle CDB=180^{\circ}-(94^{\circ}+67^{\circ})= 19^{\circ}{\small.}\) |
Келесіні аламыз
\(\displaystyle \angle BAC=\angle CDB=19^{\circ}{\small.}\)
Жауабы: \(\displaystyle б)\ 19^{\circ} {\small.}\)
