\(\displaystyle ABCD\) параллелограммының \(\displaystyle A\) және \(\displaystyle D\) бұрыштарының биссектрисалары \(\displaystyle BC \) қабырғасында жатқан \(\displaystyle M\) нүктесінде қиылысады
\(\displaystyle a) \) \(\displaystyle M\) нүктесі \(\displaystyle AB,\) \(\displaystyle AD\) және \(\displaystyle CD\) түзулерінен бірдей қашықтықта екенін дәлелдеңіз
\(\displaystyle б) \) Егер \(\displaystyle M\) нүктесінен \(\displaystyle AD\) түзуіне дейінгі қашықтық \(\displaystyle 9\) тең болса, \(\displaystyle AB\) қабырғасына жүргізілген параллелограммның биіктігін табыңыз
\(\displaystyle a) \)Есептің шартына сәйкес сызбаны орындайық.
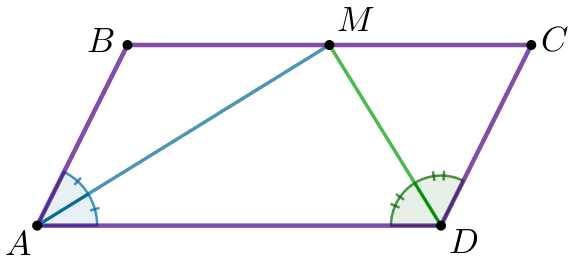 | \(\displaystyle ABCD\) – параллелограмм. \(\displaystyle AM\) – \(\displaystyle A{\small}\) бұрышының биссектрисасы \(\displaystyle DM\) – \(\displaystyle D{\small}\) бұрышының биссектрисасы \(\displaystyle M\) нүктесі \(\displaystyle BC{\small}\) қабырғасында жатыр |
\(\displaystyle M\) нүктесі \(\displaystyle AB {\small,}\) \(\displaystyle AD\) және \(\displaystyle CD {\small}\) түзулерінен бірдей қашықтықта екенін дәлелдеу қажет.
Яғни, \(\displaystyle M\) нүктесінен \(\displaystyle AB {\small,}\) \(\displaystyle AD\) және \(\displaystyle CD {\small}\) түзулеріне дейінгі арақашықтық тең екенін дәлелдеу .
Нүктеден түзуге дейінгі қашықтық – бұл берілген нүктеден түзуге түсірілген перпендикулярдың ұзындығы. Перпендикуляр – бұл нүктеден түзуге дейінгі ең қысқа қашықтық.
Қосымша сызбаларды орындайық.
\(\displaystyle M\) нүктесінен \(\displaystyle AB {\small,}\) \(\displaystyle AD\) және \(\displaystyle CD {\small}\) түзулеріне перпендикулярлар жүргіземіз
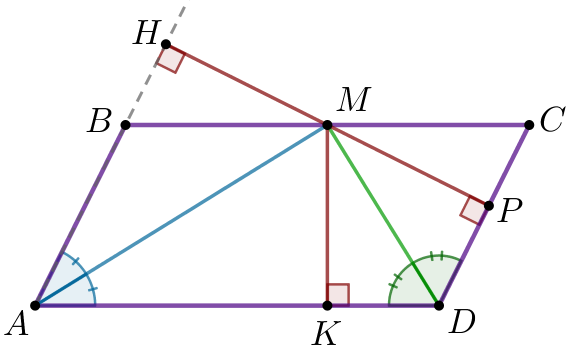 | \(\displaystyle MH \perp AB {\small;}\) \(\displaystyle MK \perp AD {\small;}\) \(\displaystyle MP \perp CD{\small.}\) \(\displaystyle MH=MK=MP{\small}\) дәлелдейік |
\(\displaystyle AMH\) және \(\displaystyle AMK{\small}\) тікбұрышты үшбұрыштарды қарастырайық
Демек, \(\displaystyle \triangle AMH=\triangle AMK\) гипотенуза және сүйір бұрыш бойынша. Тең үшбұрыштарда сәйкес қабырғалар тең болады. Яғни, \(\displaystyle MH=MK{\small.}\) | 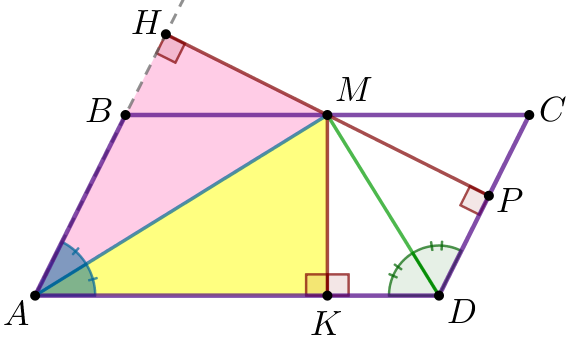 |
\(\displaystyle DMK\) және \(\displaystyle DMP{\small}\) тікбұрышты үшбұрыштарын қарастырайық
Демек, \(\displaystyle \triangle DMK=\triangle DMP\) гипотенуза және сүйір бұрыш бойынша. Тең үшбұрыштарда сәйкес қабырғалар тең болады. Яғни, \(\displaystyle MK=MP{\small.}\) | 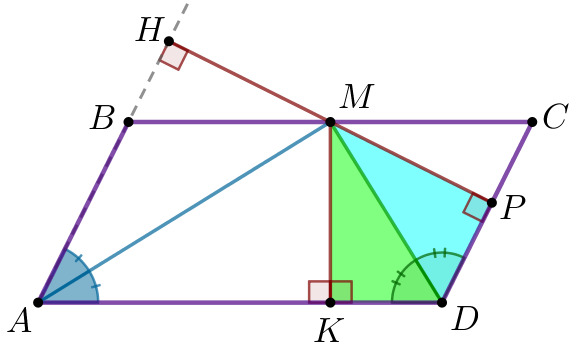 |
Келесіні аламыз
\(\displaystyle MH=MK=MP{\small.}\)
Демек, \(\displaystyle M\) нүктесі \(\displaystyle AB {\small,}\) \(\displaystyle AD\) және \(\displaystyle CD {\small}\) түзулерінен бірдей қашықтықта орналасқан.
Тұжырым дәлелденді.
\(\displaystyle б)\) Есептің шарты бойынша \(\displaystyle M\) нүктесінен \(\displaystyle AD\) түзуіне дейінгі қашықтық \(\displaystyle 9{\small}\) тең. Яғни \(\displaystyle MK=9{\small.}\)
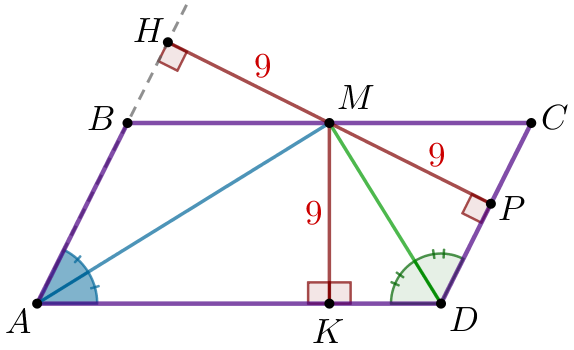 | \(\displaystyle AB \) қабырғасына жүргізілген \(\displaystyle ABCD\) параллелограммының биіктігі \(\displaystyle AB\) және \(\displaystyle CD \) параллель түзулер арасындағы қашықтыққа , яғни \(\displaystyle PH\) перпендикуляр ұзындығына тең (суретті қараңыз). \(\displaystyle PH=MP+MH{\small.}\) \(\displaystyle MH=MP=MK=9{\small}\) болғандықтан, онда \(\displaystyle PH=9+9=18{\small.}\) |
Демек, \(\displaystyle AB {\small}\) қабырғасына жүргізілген параллелограммның биіктігі \(\displaystyle 18{\small}\) тең.
Жауабы: \(\displaystyle б)\ 18 {\small.}\)
