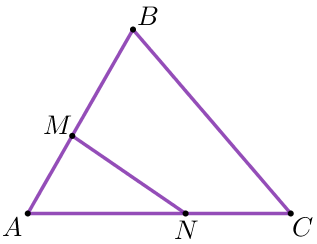
\(\displaystyle M\) және \(\displaystyle N\) нүктелері сәйкесінше үшбұрыштың \(\displaystyle ABC\) \(\displaystyle АВ\) және \(\displaystyle АС\) қабырғаларында белгіленген. \(\displaystyle AM:MB=3:4\) және \(\displaystyle AN:NC=3:2 {\small.}\) Егер үшбұрыштың ауданы \(\displaystyle AMN\) \(\displaystyle 18\) болса,\(\displaystyle ABC{\small,}\) үшбұрыштың ауданын табыңыз.
бұрыштары тең үшбұрыштардың аудандары туралы теорема
Егер бір үшбұрыштың бұрышы екінші үшбұрыштың бұрышына тең болса, онда бұл үшбұрыштардың аудандары тең бұрыштарды қоршап тұрған қабырғалардың көбейтіндісі ретінде жіктеледі: \(\displaystyle \frac{\color{blue}{S_{\triangle ABC}}}{\color{green}{S_{\triangle MNK}}}=\frac{\color{blue}{AB} \cdot \color{blue}{AC}}{\color{green}{MN} \cdot \color{green}{MK}} \) | 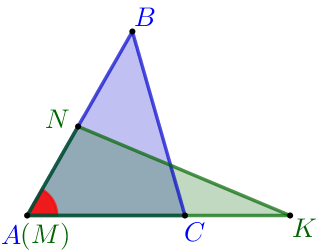 |
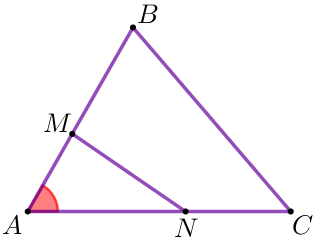 | Үшбұрыштарда \(\displaystyle AMN\) және \(\displaystyle ABC\) \(\displaystyle \angle MAN= \angle BAC {\small.}\) Бұрыштары бірдей үшбұрыштардың аудандары туралы теорема бойынша біз мынаны аламыз: \(\displaystyle \frac{S_{\triangle AMN}}{S_{\triangle ABC}}=\frac{AM \cdot AN}{AB \cdot AC} \ {\small.}\) |
Шарты бойынша \(\displaystyle \frac{AM}{MB}=\frac{3}{4} {\small.}\) Демек, \(\displaystyle \frac{AM}{AB}= \frac{AM}{AM+MB}=\frac{3}{3+4}=\frac{3}{7} {\small.} \\ \)
Өйткені \(\displaystyle \frac{AN}{NC}=\frac{3}{2} {\small,}\) содан кейін \(\displaystyle \frac{AN}{AC}= \frac{AN}{AN+NC}=\frac{3}{3+2}=\frac{3}{5} {\small.} \\ \)
Алынған бөлшектерді үшбұрыштардың аудандарының қатынасы формуласына ауыстырамыз:
\(\displaystyle \frac{S_{\triangle AMN}}{S_{\triangle ABC}}=\frac{3}{7} \cdot \frac{3}{5} \ {\small,} \\ \)
\(\displaystyle \frac{S_{\triangle AMN}}{S_{\triangle ABC}}=\frac{9}{35} \ {\small.}\)
Соңғы теңдіктен пропорционалды түрде аламыз
\(\displaystyle S_{\triangle ABC}=\frac{35 \cdot S_{\triangle AMN}}{9} \ {\small,}\)
\(\displaystyle S_{\triangle ABC}=\frac{35 \cdot 18}{9}=35 \cdot 2=70 {\small.}\)
Жауабы: \(\displaystyle 70 {\small.}\)
