Үшбұрышта \(\displaystyle ABC\) бұрышы \(\displaystyle C\) \(\displaystyle 90^{\circ}{\small , }\) қабырғаларының ұзындығы \(\displaystyle AB=10 {\small , }\) \(\displaystyle BC=6 {\small .}\) Үшбұрыштың ауданын табыңыз
Тікбұрышты үшбұрыштың ауданы катеттерінің ұзындықтарының көбейтіндісінің жартысына тең:
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot AC\cdot BC{\small .}\)
Қабырғасын табайық \(\displaystyle AC{\small .}\)
Пифагор теоремасы бойынша бізде: \(\displaystyle AC^2+BC^2=AB^2{\small .}\) \(\displaystyle AB=10\) және \(\displaystyle BC=6\) теңдікке ауыстырсақ, мынаны аламыз: \(\displaystyle AC^2+6^2=10^2{\small , }\) \(\displaystyle AC^2+36=100{\small , }\) \(\displaystyle AC^2=100-36=64{\small , }\) Кесіндінің ұзындығы оң болғандықтан \(\displaystyle AC=8{\small . }\) | 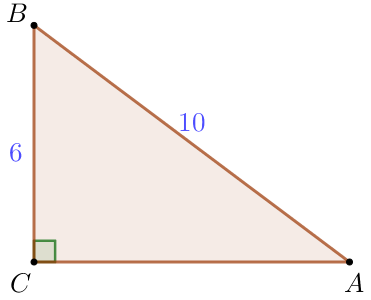 |
Тікбұрышты үшбұрыштың ауданы формуласына \(\displaystyle AC=8\) және \(\displaystyle BC=6\) ауыстырыңыз:
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot 8\cdot 6{\small , }\)
\(\displaystyle S_{ABC}=24{\small .}\)
Жауабы: \(\displaystyle 24{\small .}\)
