Шеңбер секторының ауданын табыңыз.
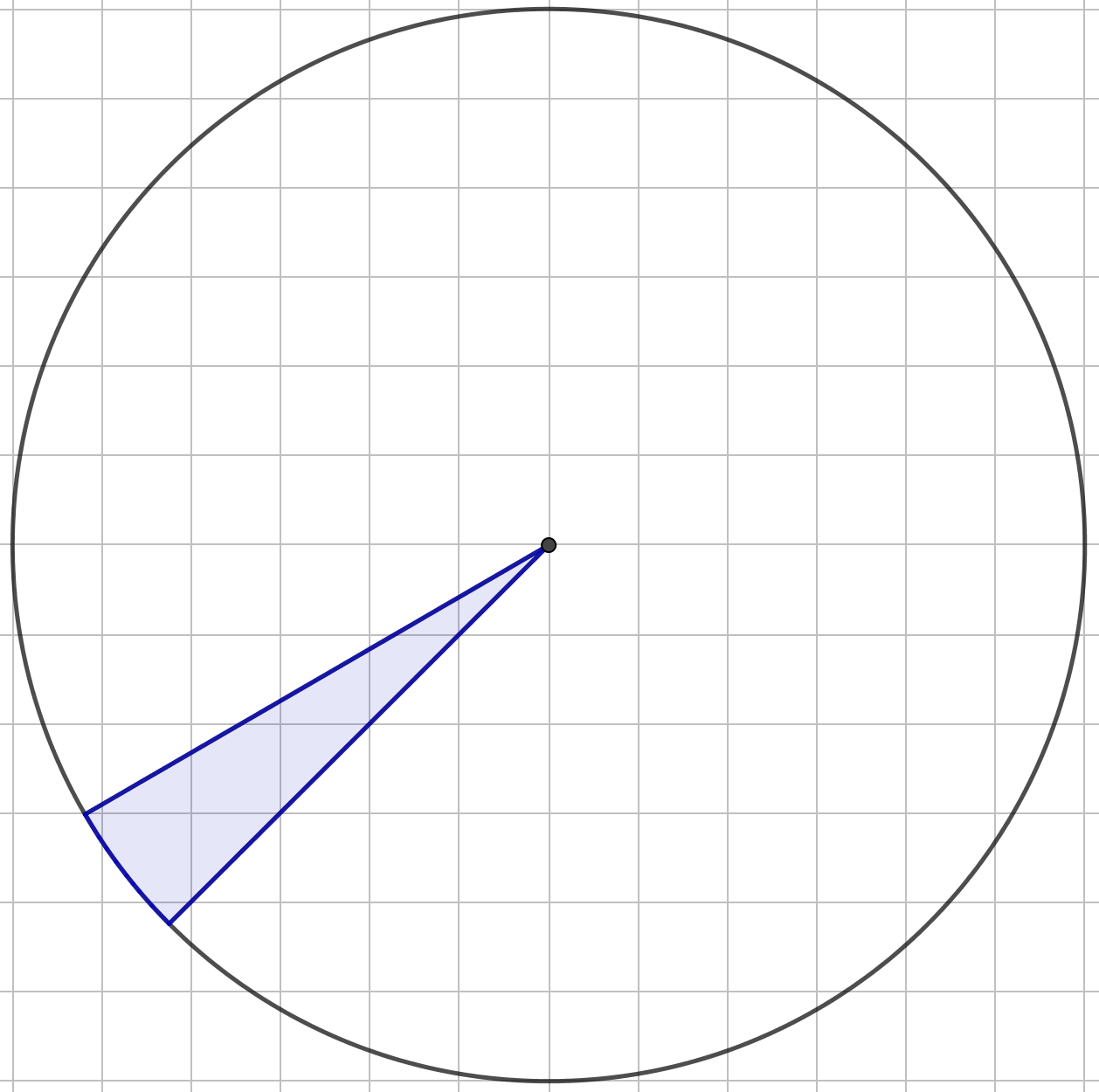
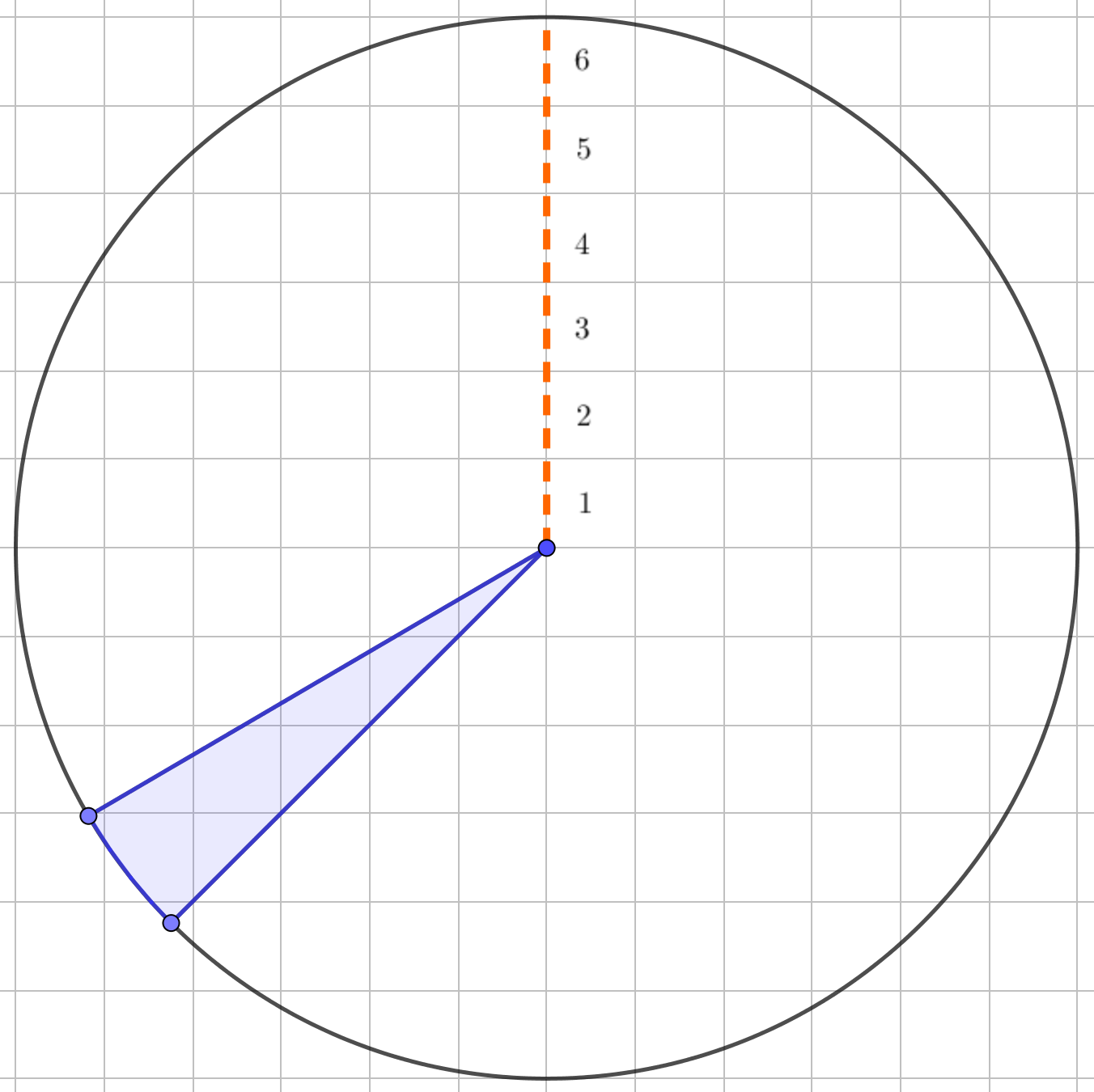
Суреттен берілген шеңбердің радиусы \(\displaystyle 6\) бірлікке тең екенін көруге болады:
Қызыл үшбұрышты қарастырайық:
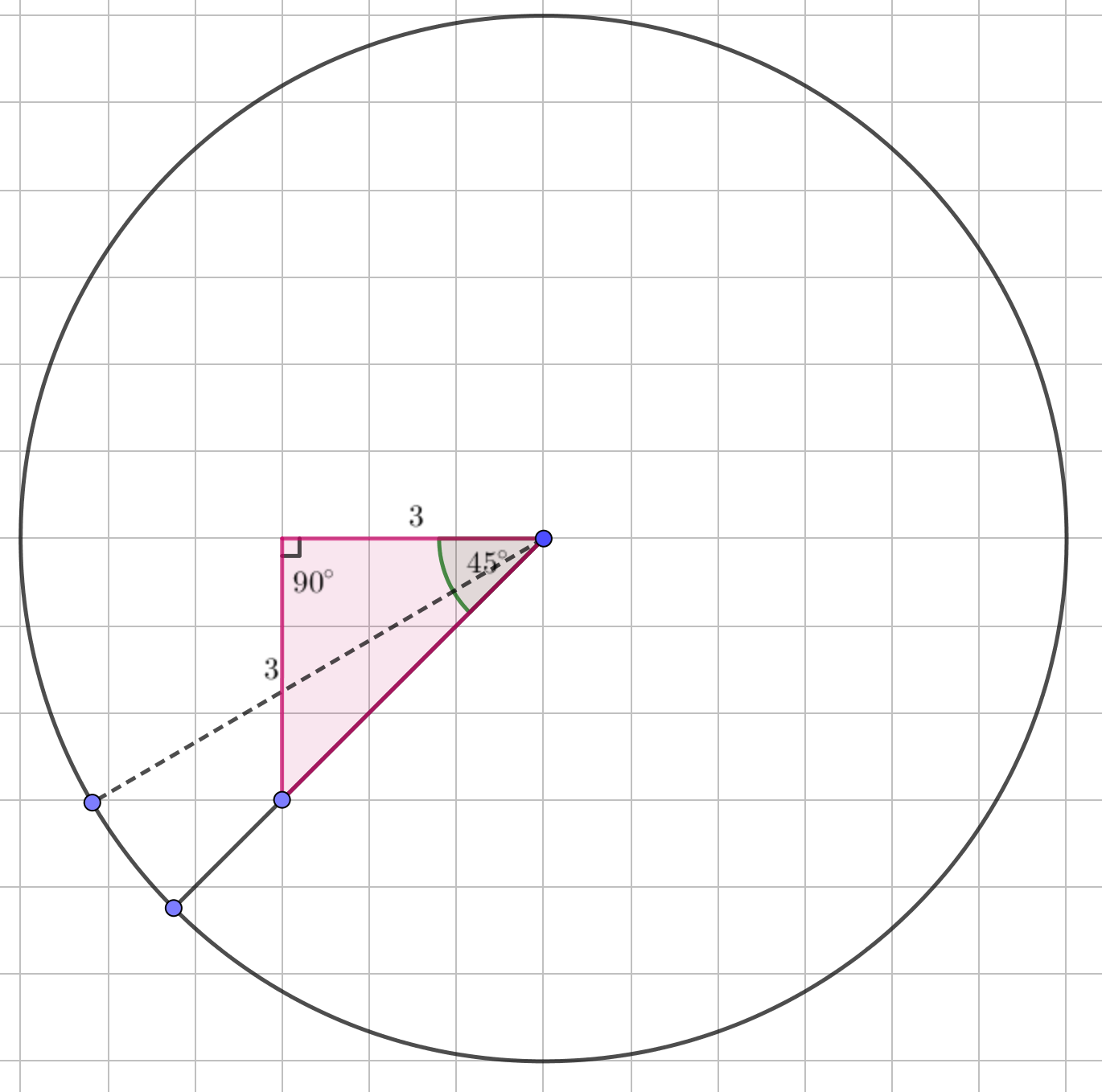
Бұл теңбүйірлі тікбұрышты үшбұрыш. Демек, табанындағы бұрыш \(\displaystyle 45^{\circ}\) немесе \(\displaystyle \frac{\pi}{4}\) радианға тең.
Бұрыштың екінші жағында қосымша (жасыл) тікбұрышты үшбұрыш салайық:
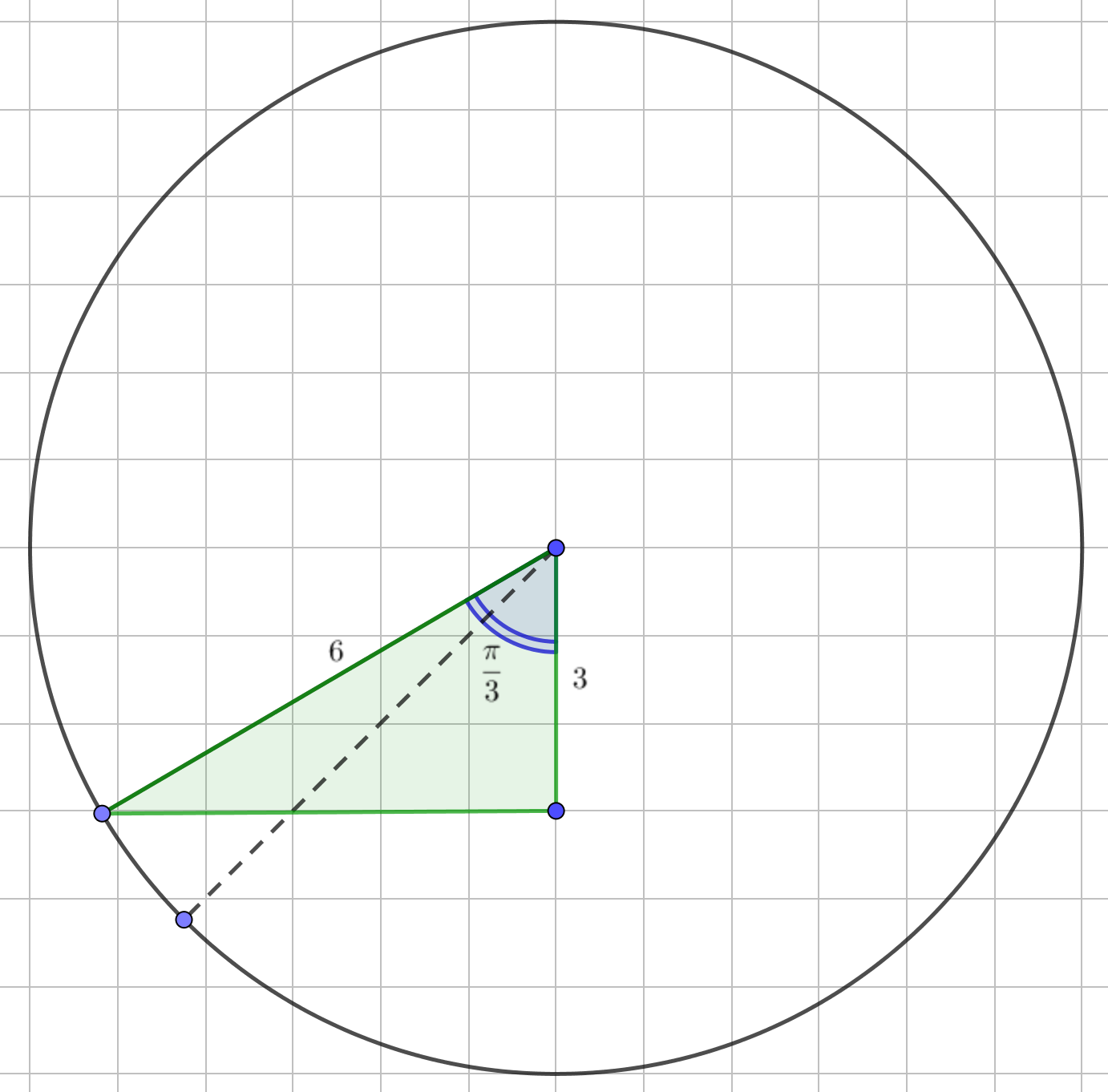
Суреттен катеттердің бірі \(\displaystyle 3{ \small ,}\) ал гипотенуза радиус, яғни \(\displaystyle 6{\small }\) тең екенін көруге болады Онда ізделініп отырған бұрыштың косинусы
\(\displaystyle \cos( \color{blue}{көк\, бұрыш})=\frac{3}{6}=\frac{1}{2}{\small .}\)
Демек, ізделініп отырған көк бұрыш \(\displaystyle \frac{\pi}{3}{\small .}\)
Әрі қарай табылған екі бұрышты да қарастырайық:
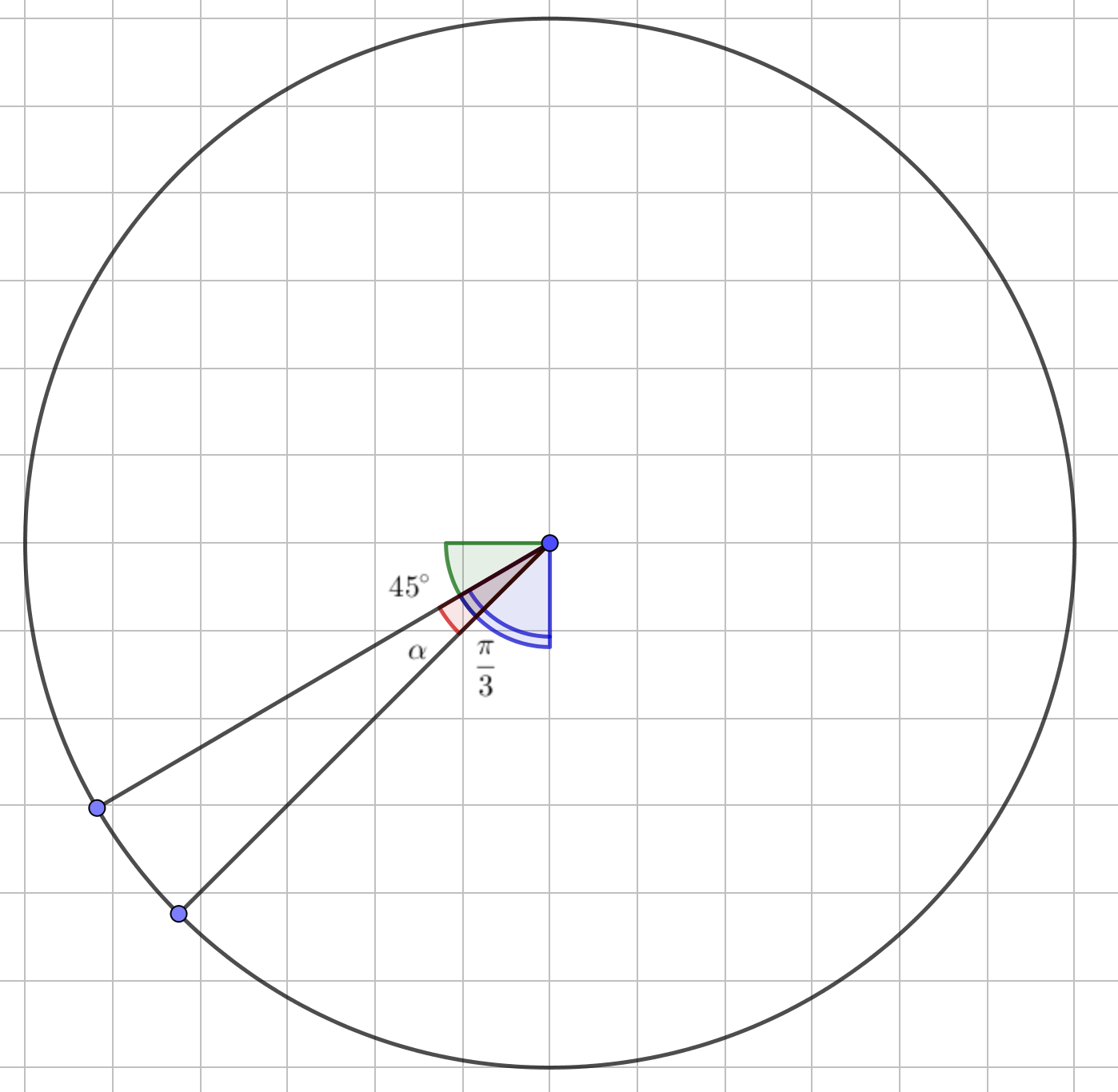
Олардың \(\displaystyle \alpha{\small }\) ортақ бұрышы бар
Суреттен егер \(\displaystyle \frac{\pi}{4}{ \small ,}\) тең жасыл бұрышты және \(\displaystyle \frac{\pi}{3}{ \small ,}\) тең көк бұрышты қоссақ, онда олардың қосындысы \(\displaystyle \frac{\pi}{2}+\alpha{\small }\) тең болатыны шығады
\(\displaystyle \alpha\) – бұрышы – бұл бұрыштардың қиылысы және ол екі рет саналатындықтан, онда
\(\displaystyle \frac{\pi}{4}+\frac{\pi}{3}=\frac{\pi}{2}+\alpha{ \small ,}\)
\(\displaystyle \alpha=\frac{\pi}{4}+\frac{\pi}{3}-\frac{\pi}{2}{ \small ,}\)
\(\displaystyle \alpha=\frac{\pi}{12}{\small .}\)
\(\displaystyle \alpha\) бұрышымен \(\displaystyle R\) радиус шеңбері секторының аудан формуласы
\(\displaystyle S=\alpha \cdot \frac{R^2}{2}{\small .}\)
Осылайша ізделініп отырған сектордың ауданы
\(\displaystyle S=\frac{\pi}{12}\cdot \frac{6^2}{2}=\frac{36\pi}{24}=\frac{3\pi}{2}{\small .}\)
Жауабы:\(\displaystyle \frac{3\pi}{2}{\small .}\)
