\(\displaystyle O\) нүктесі – \(\displaystyle ABCD\) ромбының \(\displaystyle AC\) және \(\displaystyle BD\) диагональдарының қиылысу нүктесі. Егер \(\displaystyle ABO\) үшбұрыштың ауданы \(\displaystyle 10\)- ға тең болса, ромбтың ауданын табыңыз.
Ромбтың қасиеті бойынша диагональдар \(\displaystyle AC\) және \(\displaystyle BD\) перпендикуляр, параллелограмм қасиеті бойынша олар \(\displaystyle O \small\) нүктесімен бөлінген. Содан кейін тікбұрышты үшбұрыштар \(\displaystyle AOB \small,\) \(\displaystyle COB \small,\) \(\displaystyle COD\) және \(\displaystyle AOD\) екі катетпен тең.
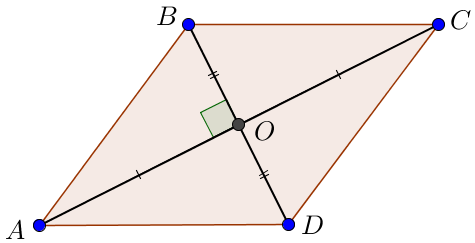
Демек, \(\displaystyle AOB \small,\) \(\displaystyle BOC \small,\) \(\displaystyle COD\) және \(\displaystyle DOA\) үшбұрыштарының аудандары тең және
\(\displaystyle S_{ABCD}={4} \cdot S_{ABO}=4 \cdot 10= 40 \small.\)
Жауабы: \(\displaystyle 40 {\small .}\)
