1) \\(\displaystyle f(x)=\left(x^2-7x+13\right)e^{x-4}{\small}\) функциясының туындысын табыңыз.
\(\displaystyle f^{\prime}(x)=\left(\left(x^2-7x+13\right)e^{x-4}\right)^{\prime}=(2x-7)e^{x-4}+\left(x^2-7x+13\right)e^{x-4}{\small.}\)
Дифференциалдау ережесін қолданайық:
ПравилоӨнім туындысы
\(\displaystyle\left(\color{green}{f(x)}\cdot\color{blue}{g(x)}\right)^{\prime}=\left(\color{green}{f(x)}\right)^{\prime}\cdot\color{blue}{g(x)}+\color{green}{f(x)}\cdot\left(\color{blue}{g(x)}\right)^{\prime}{\small.}\)
Аламыз
\(\displaystyle\left(\color{green}{\left(x^2-7x+13\right)}\cdot\color{blue}{e^{x-4}}\right)^{\prime}=\left(\color{green}{x^2-7x+13}\right)^{\prime}\cdot\color{blue}{e^{x-4}}+\left(\color{green}{x^2-7x+13}\right)\cdot\left(\color{blue}{e^{x-4}}\right)^{\prime}{\small.}\)
Туындыны \(\displaystyle x^2-7x+13\) есептеңдер
\(\displaystyle \color{green}{\left(x^2-7x+13\right)^{\prime}=\left(x^2\right)^{\prime}-(7x)^{\prime}+(13)^{\prime}=2x-7{\small.}}\)
Аламыз:
\(\displaystyle\color{green}{\left(x^2-7x+13\right)^{\prime}}\cdot{e^{x-4}}+{\left(x^2-7x+13\right)}\cdot\left({e^{x-4}}\right)^{\prime}=\color{green}{(2x-7)}\cdot{e^{x-4}}+{\left(x^2-7x+13\right)}\cdot\left({e^{x-4}}\right)^{\prime}{\small.}\)
Күрделі \(\displaystyle e^{x-4}{\small}\) функцияның туындысын табу керек
Ережені қолдана отырып, оны кезең-кезеңімен орындайық.
ПравилоКүрделі функцияның туындысы
\(\displaystyle \left(h({g(x)})\right)^{\prime}=\color{red}{h^{\prime}(g)}\cdot (\color{blue}{g(x)})'{\small.}\)
Әрбір кезеңнің міндеті \(\displaystyle h(g(x))\) функциясының туындысын қарапайым функцияның \(\displaystyle g(x){\small}\) туындысын есептеуге келтіру.
1-кезең. \(\displaystyle h(g(x))=e^{x-4}{\small}\) деп белгілеңіз. Сонда:
\(\displaystyle \boxed{h(\color{blue}{g(x)})=e^{\color{blue}{x-4}}}\longrightarrow\) \(\displaystyle \boxed{ \begin{aligned}&h(x)=e^x\\&\color{blue}{g(x)=x-4}\end{aligned}}\longrightarrow\) \(\displaystyle \boxed{\begin{aligned}&h^{\prime}(x)=(e^x)^{\prime}=e^x\\&\color{red}{h^{\prime}(g)=e^{x-4}}\end{aligned}} \longrightarrow\)
\(\displaystyle \longrightarrow\boxed{\begin{aligned}\left(e^{x-4}\right)^{\prime}=\color{red}{e^{x-4}}\cdot\left(\color{blue}{x-4}\right)^{\prime}\end{aligned}{\small.}}\)
Алынған:
\(\displaystyle (2x-7){e^{x-4}}+\left(x^2-7x+13\right)\cdot\left({e^{x-4}}\right)^{\prime}=(2x-7){e^{x-4}}+\left(x^2-7x+13\right)\cdot\left({e^{x-4}}\right)\cdot(x-4)^{\prime}{\small.}\)
Қарапайым функцияның туындысын есептеуге көшейік \(\displaystyle x-4{\small.}\)
2-кезең. \(\displaystyle \left({x-4}\right)^{\prime}=(x)^{\prime}-(4)^{\prime}=1-0=1{\small}\) болғандықтан мынаны аламыз:
\(\displaystyle \begin{aligned}(2x-7){e^{x-4}}+\left(x^2-7x+13\right){e^{x-4}}\cdot(x-4)^{\prime}=(2x-7){e^{x-4}}+\left(x^2-7x+13\right){e^{x-4}}\cdot1=\\[5px]=(2x-7){e^{x-4}}+\left(x^2-7x+13\right){e^{x-4}}{\small.}\end{aligned}\)
Сонымен \(\displaystyle \left(x^2-7x+13\right)e^{x-4}\) функциясының туындысын алу процесі келесідей:
\(\displaystyle \begin{aligned}&\left(\left(x^2-7x+13\right)e^{x-4}\right)^{\prime}=\left(\left(x^2-7x+13\right)\right)^{\prime}\cdot e^{x-4}+\left(x^2-7x+13\right)\left(e^{x-4}\right)^{\prime}=\\[5px]&=(2x-7){e^{x-4}}+\left(x^2-7x+13\right)\cdot\left({e^{x-4}}\right)\cdot(x-4)^{\prime}=(2x-7){e^{x-4}}+\left(x^2-7x+13\right){e^{x-4}}{\small.}\end{aligned}\)
Өрнекті \(\displaystyle (2x-7)e^{x-4}+\left(x^2-7x+13\right)e^{x-4}{\small}\) жеңілдету
\(\displaystyle e^{x-4}\) жақшаның ішінен шығарайық, содан кейін ұқсас шарттарды берейік:
\(\displaystyle \begin{aligned}(2x-7)e^{x-4}+\left(x^2-7x+13\right)e^{x-4}=\left(\color{red}{\underline{\color{black}{2x}}}-{\color{red}{\underline{\underline{\color{black}{7}}}}}+\color{red}{\underline{\underline{\underline{\color{black}{x^2}}}}}-\color{red}{\underline{\color{black}{7x}}}+{\color{red}{\underline{\underline{\color{black}{13}}}}}\right)e^{x-4}=\\[10px]=\left(\color{red}{\underline{\underline{\underline{\color{black}{x^2}}}}}-\color{red}{\underline{\color{black}{5x}}}+{\color{red}{\underline{\underline{\color{black}{6}}}}}\right)e^{x-4}{\small.}\end{aligned}\)
Осылайша, біз аламыз:
\(\displaystyle f^{\prime}(x)=(2x-7)e^{x-4}+\left(x^2-7x+13\right)e^{x-4}=\left(x^2-5x+6\right)e^{x-4}{\small.}\)
2) \(\displaystyle f^{\prime}(x)=0{\small}\) болатын нүктелерді табайық.
\(\displaystyle f^{\prime}(x)=\left(x^2-5x+6\right)e^{x-4}{\small}\) болғандықтан, ол үшін теңдеуді шешу керек.
\(\displaystyle \left(x^2-5x+6\right)e^{x-4}=0{\small.}\)
\(\displaystyle x_1=3\) және \(\displaystyle x_2=2\) теңдеуінің түбірлері \(\displaystyle \left(x^2-5x+6\right)e^{x-4}=0{\small.}\)
Егер \(\displaystyle \left(x^2-5x+6\right)e^{x-4}=0{\small}\) болса, онда факторлардың кем дегенде біреуі нөлге тең:
\(\displaystyle e^{x-4}=0{\small,}\) шешімдер жоқ. |
\(\displaystyle x^2-5x+6=0{ \small .}\)
Дискриминантты есептейік: \(\displaystyle D=(-5)^2-4\cdot1\cdot6=25-24=1\)
и
\(\displaystyle \sqrt{D}=\sqrt{1}=1{\small.}\) Теңдеудің түбірлерін табайық: \(\displaystyle x_1=\frac{-(-5)+1}{2}=\frac{6}{2}=3{\small,}\) \(\displaystyle x_2=\frac{-(-5)-1}{2}=\frac{4}{2}=2{\small.}\) |
3) Туындының түбірлерін нақты түзуде белгілейміз, сонымен қатар оның пайда болған интервалдардағы белгілерін анықтаймыз.


- \(\displaystyle \color{green}{(-\infty;\,2)}\) және \(\displaystyle \color{Purple}{(3;\,+\infty)}\) аралықтарында \(\displaystyle f^{\prime}(x)>0{\small,}\)
- интервалында \(\displaystyle \textcolor{blue}{(2;\, 3)}\) функциясы \(\displaystyle f^{\prime}(x)<0{\small.}\)
Функцияның \(\displaystyle f^{\prime}(x)=\left(x^2-5x+6\right)e^{x-4}\) әрбір интервалдағы таңбасын анықтайық:
\(\displaystyle \color{green}{(-\infty;\,2)}{\small,}\) \(\displaystyle \color{blue}{(2;\, 3)}{\small,}\) \(\displaystyle \textcolor{Purple}{(3;\, +\infty)}{\small.}\)
Ол үшін интервалдардың әрқайсысынан нүктені таңдаймыз және осы нүктедегі функцияның таңбасын анықтаймыз.
Кез келген дәрежеде \(\displaystyle e \) нөлден үлкен екенін ескерсек, мынаны аламыз:
- \(\displaystyle \color{green}{x=1\in(-\infty;\,2)}\) белгісі үшін \(\displaystyle f^{\prime}(\color{green}{1})=(1^2-5\cdot1+6)e^{1-4}=(1-5+6)e^{-3}\color{red}{>}0{\small ;}\)
- \(\displaystyle \color{blue}{x=2{,}5\in(2;\, 3)}\) белгісі үшін \(\displaystyle f^{\prime}(\color{blue}{2{,}5})=(2{,}5^2-5\cdot2{,}5+6)e^{2{,}5-4}=(6{,}25-12{,}5+6)e^{1{,}5}\color{red}{<}0{\small ;}\)
- \(\displaystyle \textcolor{Purple}{x=4\in(3;\, +\infty)}\) белгісі үшін \(\displaystyle f^{\prime}(\textcolor{Purple}{4})=(4^2-5\cdot4+6)e^{4-4}=16-20+6\textcolor{red}{>}0{\small.}\)
білдіреді,
- \(\displaystyle \color{green}{(-\infty;\,2)}\) және \(\displaystyle \color{Purple}{(3;\,+\infty)}\) аралықтарында \(\displaystyle f^{\prime}(x)>0{\small,}\)
- интервалында \(\displaystyle \textcolor{blue}{(2;\, 3)}\) функциясы \(\displaystyle f^{\prime}(x)<0{\small.}\)
Суреттегі туындының белгілерін белгілей отырып, біз аламыз:

4)\(\displaystyle f(x)=\left(x^2-7x+13\right)e^{x-4}{\small}\)ережені пайдаланып функцияның өсу және кему аралықтарын анықтайық.
ПравилоЕгер кез келген нүкте үшін \(\displaystyle x_0\in(a;\,b)\) туынды \(\displaystyle f'(x_0)\) бар болса және \(\displaystyle f'(x_0)>0{\small}\) болса, онда
\(\displaystyle f(x)\) функциясы бүкіл интервалда \(\displaystyle (a;\,b){\small}\) өсуде \(\displaystyle \nearrow\)
Егер кез келген нүкте үшін \(\displaystyle x_0\in(a;\,b)\) туынды \(\displaystyle f'(x_0)\) бар болса және \(\displaystyle f'(x_0)<0{\small}\) болса, онда
\(\displaystyle f(x)\) функциясы бүкіл интервалда \(\displaystyle (a;\,b){\small}\) кемуде \(\displaystyle \searrow\)
\(\displaystyle f'(x){\small}\) туындының белгілерін білу \(\displaystyle f(x){\small}\) өсу және кему аралықтарын анықтау
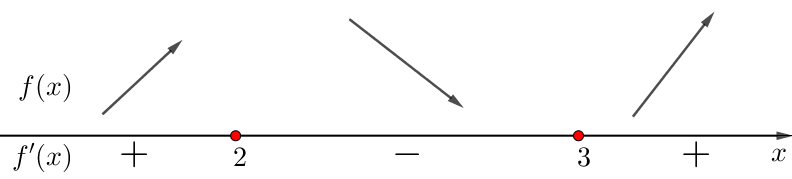
Схемалық \(\displaystyle f(x){\small}\) түрде көрсетіңіз
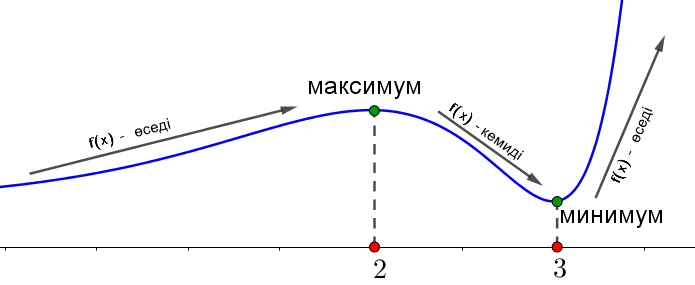
Демек, \(\displaystyle x=2\) – функцияның ең үлкен нүктесі \(\displaystyle f(x)=\left(x^2-7x+13\right)e^{x-4}{\small.}\)
Ал \(\displaystyle x=3\) – ең төменгі нүкте.
5) \(\displaystyle \left[0;\,4\right]\) аралық нүктелерінің қайсысында максималды мәнге жеткенін анықтайық.
Суреттегі \(\displaystyle \left[0;\,4\right]{\small}\) интервалға назар аударыңыз
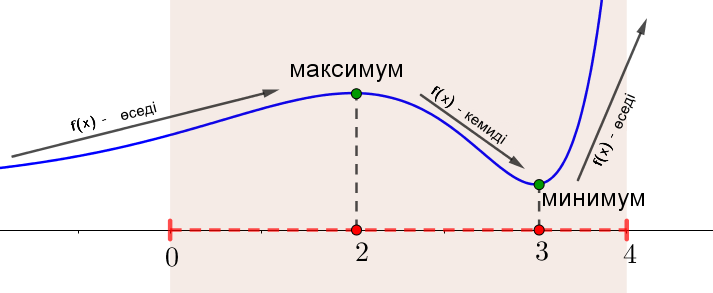
\(\displaystyle \left[0;\,4\right]\) кесіндісінде \(\displaystyle f(x)\) функциясының максималды мәніне не максималды нүктеде \(\displaystyle \color{green}{x={2}}{\small}\) не оң жағында \(\displaystyle \color{blue}{x=4}{\small}\) жететінін көруге болады.
Осы нүктелердегі мәндерді есептеп, оларды салыстырайық:
\(\displaystyle f\left(\color{green}{2}\right)=(2^2-7\cdot2+13)e^{2-4}=(4-14+13)\cdot e^{-2}={3e^{-2}}=\color{green}{\frac{3}{e^2}}{\small,}\)
\(\displaystyle f(\color{blue}{4})=(4^2-7\cdot4+13)e^{4-4}=16-28+13=\color{blue}{1}{\small.}\)
\(\displaystyle e>2{\small}\) бастап,
\(\displaystyle \color{green}{\frac{3}{e^2}}<\frac{3}{2^2}=\frac{3}{4}<\color{blue}{1}{\small.}\)
Яғни, \(\displaystyle f(\color{green}{2})<f(\color{blue}{4}){\small.}\)
Демек, \(\displaystyle \color{blue}{x=4}\) нүктесінде максималды мәнге жетеді және ол \(\displaystyle f(\color{blue}{4})=\color{blue}{1}\) тең болады.
Жауабы: \(\displaystyle 1{\small.}\)


