1) \(\displaystyle f(x)=12\cos x+6\sqrt{3} x-2\sqrt{3}\pi +6{\small}\) функциясының туындысын табыңыз.
\(\displaystyle f^{\prime}(x)=\left(12\cos x+6\sqrt{3} x-2\sqrt{3}\pi +6\right)^{\prime}=-12\sin x + 6\sqrt{3}{\small.}\)
\(\displaystyle \begin{aligned}(12\cos x+6\sqrt{3} x-2\sqrt{3}\pi +6)^{\prime}=(12\cos x)^{\prime}+(6\sqrt{3} x)^{\prime}-(2\sqrt{3}\pi)^{\prime}+(6)^{\prime}=\\[5px]=12\cdot(\cos x)^{\prime}+6\sqrt{3}\cdot(x)^{\prime}-(2\sqrt{3}\pi)^{\prime} +(6)^{\prime}=-12\sin x+6\sqrt{3}{\small.}\end{aligned}\)
2) \(\displaystyle f^{\prime}(x)=0{\small}\) нүктелерін табыңыз.
\(\displaystyle f^{\prime}(x)=-12\sin x+6\sqrt{3}{\small}\) болғандықтан, бұл үшін теңдеуді шешу керек.
\(\displaystyle -12\sin x+6\sqrt{3}=0{\small.}\)
\(\displaystyle x_1=\frac{\pi}{3}+2\pi n{\small,}\,\, n \in \mathbb{Z}\) және \(\displaystyle x_2=\frac{2\pi}{3}+2\pi m{\small,}\,\, m \in \mathbb{Z}\) корни уравнения \(\displaystyle -12\sin x+6\sqrt{3}=0{\small.}\)
Өйткені \(\displaystyle -12\sin x+6\sqrt{3}=0{\small}\) онда\(\displaystyle -12\sin x=-6\sqrt{3}\) және \(\displaystyle \sin x = \frac{\sqrt{3}}{2}{\small.}\)
Қарапайым тригонометриялық теңдеуді шешейік \(\displaystyle \sin x = \frac{\sqrt{3}}{2}{\small.}\)
Синустың мәндері \(\displaystyle \rm OY{\small}\) осьте жатқандықтан, онда түзу сызықты \(\displaystyle y=\frac{\sqrt{3}}{2}\) және тригонометриялық шеңберді қиып өтеміз.
\(\displaystyle \sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}{\small}\) болғандықтан, жасыл бұрыш \(\displaystyle \frac{\pi}{3}{\small}\) тең, ал қызыл бұрыш \(\displaystyle \pi-\frac{\pi}{3}\text{=}\frac{2\pi}{3}{\small}\) тең болады.
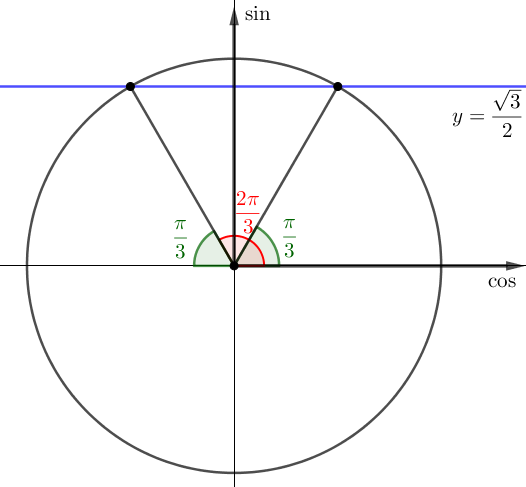
Біз шешімдердің екі жиынтығын аламыз:
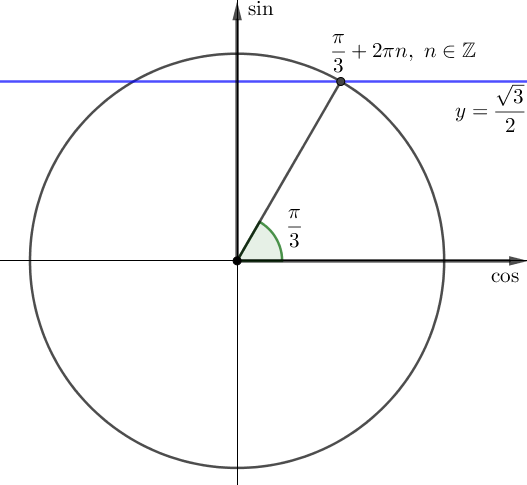 | 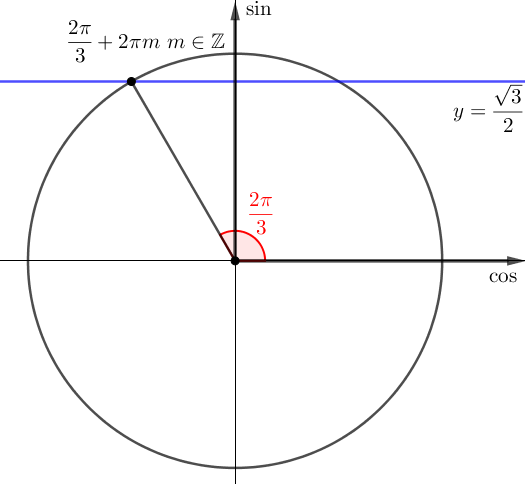 |
| \(\displaystyle x_1=\frac{\pi}{3}+2\pi n{\small,}\,\, n \in \mathbb{Z}\) | \(\displaystyle x_2=\frac{2\pi}{3}+2\pi m{\small,}\,\, m \in \mathbb{Z}\) |
3) Түбірлер жиынынан \(\displaystyle \left[0;\frac{\pi }{2}\right]{\small}\) аралықта жататындарды таңдаймыз.
\(\displaystyle x=\frac{\pi}{3}\) сегментте жатқан теңдеудің түбірі \(\displaystyle -12\sin x+6\sqrt{3}=0{\small}\) \(\displaystyle [ 0;\frac{\pi }{2} ]{\small.}\)
Тригонометриялық шеңберді тұрғызайық. Оның үстіне шешімдерге сәйкес нүктені \(\displaystyle x_1=\frac{\pi}{3}+2\pi n{\small,}\,\, n \in \mathbb{Z}{\small}\) және шешімдерге сәйкес нүктені \(\displaystyle x_2=\frac{2\pi}{3}+2\pi m{\small,}\,\, m \in \mathbb{Z}{\small}\) белгілейміз
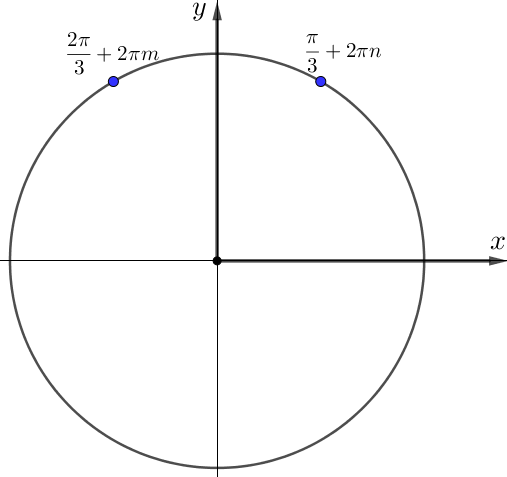
Бірлік шеңбердегі кесіндіні \(\displaystyle \left[ 0;\frac{\pi }{2} \right]{\small}\) белгілейік, мынаны аламыз:
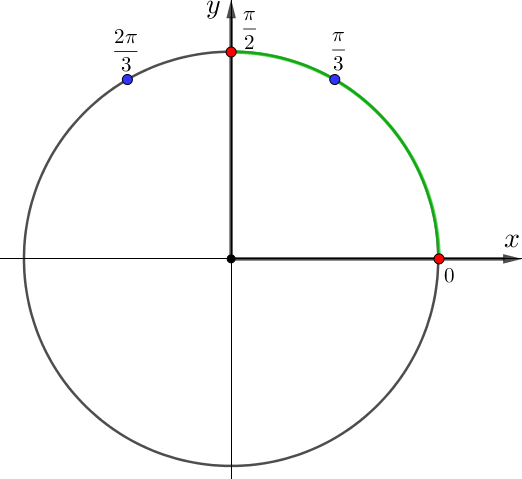
Демек, \(\displaystyle \left[ 0;\frac{\pi }{2} \right]\) кесіндісінде бір түбір бар \(\displaystyle x=\frac{\pi}{3}{\small.}\)
4) Сан жолында туындының түбірлерін \(\displaystyle x_1=\frac{\pi}{3}+2\pi n{\small,}\,\, n \in \mathbb{Z}\) және \(\displaystyle x_2=\frac{2\pi}{3}+2\pi m{\small,}\,\, m \in \mathbb{Z}\) белгілеңіз.
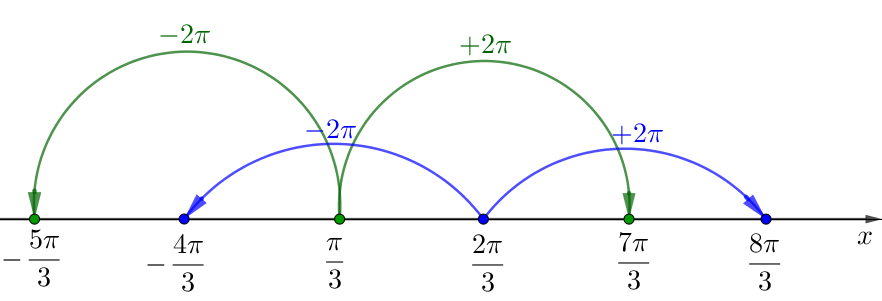
Біз сегменттегі функцияның ең үлкен мәнін іздейтіндіктен \(\displaystyle \left[ 0;\frac{\pi }{2} \right]{\small}\) біз мынаны аламыз:
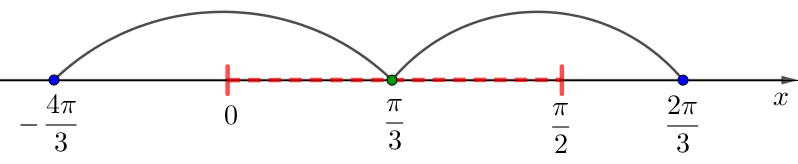
\(\displaystyle \left(-\frac{4\pi}{3};\,\frac{\pi}{3}\right)\) және \(\displaystyle \left(\frac{\pi}{3};\, \frac{2\pi}{3}\right)\) аралықтары бойынша туындының таңбаларын табыңыз.
- \(\displaystyle \color{green}{\left(-\frac{4\pi}{3};\,\frac{\pi}{3}\right)}\) функциясы \(\displaystyle f^{\prime}(x)>0{\small}\) интервалында,
- интервалында \(\displaystyle \color{blue}{\left(\frac{\pi}{3};\, \frac{2\pi}{3}\right)}\) функциясы \(\displaystyle f^{\prime}(x)<0{\small.}\)
\(\displaystyle f^{\prime}(x)=-12\sin x+6\sqrt{3}\) функциясының әрбір интервалдағы таңбасы анықталсын:
\(\displaystyle \color{green}{\left(-\frac{4\pi}{3};\,\frac{\pi}{3}\right)}{\small,}\) \(\displaystyle \color{blue}{\left(\frac{\pi}{3};\, \frac{2\pi}{3}\right)}{\small.}\)
Ол үшін интервалдардың әрқайсысынан нүктені таңдаймыз және осы нүктедегі функцияның таңбасын анықтаймыз. Аламыз:
- \(\displaystyle \color{green}{x=0 \in \left(-\frac{4\pi}{3};\,\frac{\pi}{3}\right)}\) белгісі үшін \(\displaystyle f^{\prime}(\color{green}{0})=-12\sin 0+6\sqrt{3}=6\sqrt{3}\color{red}{>}0{\small ;}\)
- \(\displaystyle \color{blue}{x=\frac{\pi}{2} \in{\left(\frac{\pi}{3};\, \frac{2\pi}{3}\right)}}\) белгісі үшін \(\displaystyle f^{\prime}\left(\color{blue}{\frac{\pi}{2}}\right)=-12\sin \frac{\pi}{2}+6\sqrt{3}=-12+6\sqrt{3}=6(\sqrt{3}-2)\color{red}{<}0{\small .}\)
білдіреді,
- \(\displaystyle \color{green}{\left(-\frac{4\pi}{3};\,\frac{\pi}{3}\right)}\) функциясы \(\displaystyle f^{\prime}(x)>0{\small}\) интервалында,
- интервалында \(\displaystyle \color{blue}{\left(\frac{\pi}{3};\, \frac{2\pi}{3}\right)}\) функциясы \(\displaystyle f^{\prime}(x)<0{\small.}\)
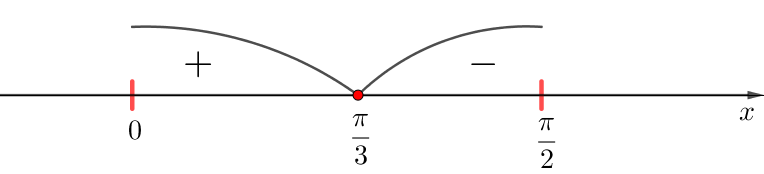
Суреттегі туындының белгілерін белгілей отырып, біз аламыз:
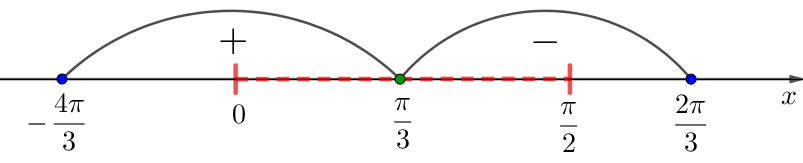
Демек, \(\displaystyle {\left(0;\,\frac{\pi}{3}\right)}\) интервалында туынды оң \(\displaystyle {\left(\frac{\pi}{3};\, \frac{\pi}{2}\right)}\) аралығында туынды теріс болады:
5) Ережені пайдаланып \(\displaystyle f(x)=12\cos x+6\sqrt{3} x-2\sqrt{3}\pi +6{\small}\) функциясының өсу және кему аралықтарын анықтайық.
ПравилоЕгер кез келген нүкте үшін \(\displaystyle x_0\in(a;\,b)\) туынды \(\displaystyle f'(x_0)\) бар және \(\displaystyle f'(x_0)>0{\small}\) болса, онда
\(\displaystyle f(x)\) бүкіл интервалда артады ( seаrrow ) \(\displaystyle (a;\,b){\small.}\)
Егер кез келген нүкте үшін \(\displaystyle x_0\in(a;\,b)\) туынды \(\displaystyle f'(x_0)\) бар және \(\displaystyle f'(x_0)<0{\small}\) болса, онда
\(\displaystyle f(x)\) кемиді ( seаrrow ) бүкіл интервалда \(\displaystyle (a;\,b){\small.}\)
Туындының \(\displaystyle f'(x){\small}\) белгілерін біле отырып, өсу және кему аралықтарын \(\displaystyle f(x){\small}\) анықтаймыз.
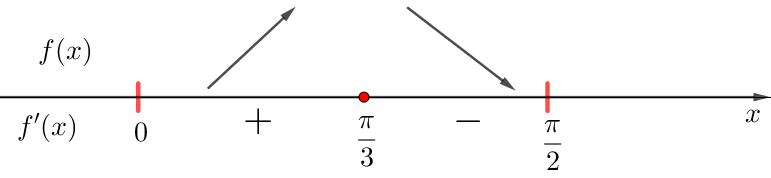
6) Схемалық түрде \(\displaystyle f(x)\) аралығында \(\displaystyle \left[ 0;\frac{\pi }{2} \right]{\small}\) бейнелеу:
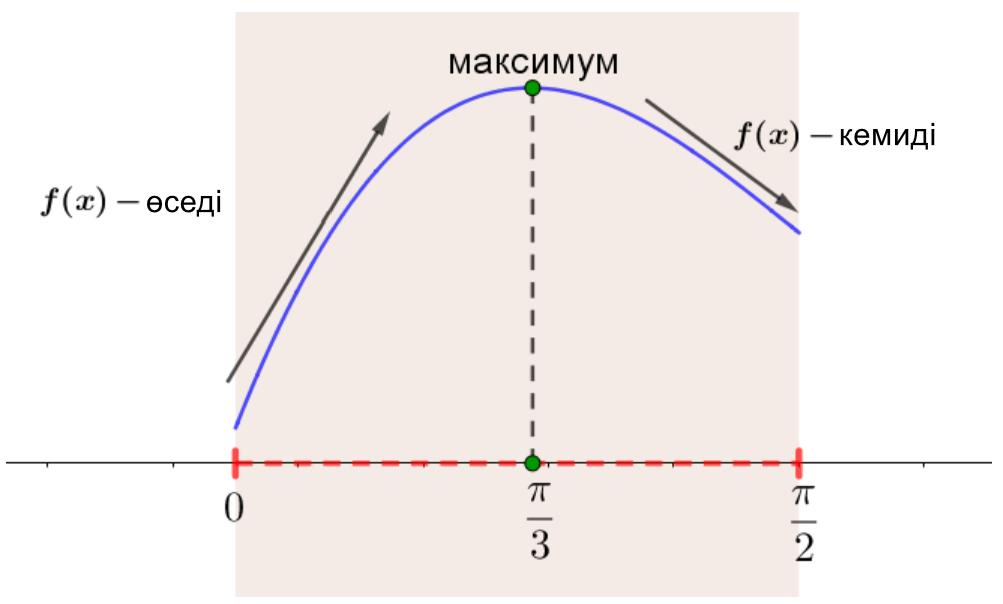
\(\displaystyle \left[ 0;\frac{\pi }{2} \right]\) аралықта функцияның \(\displaystyle x=\frac{\pi}{3}{\small}\) нүктесіне дейін өсетінін, содан кейін төмендейтінін көруге болады.
Бұл \(\displaystyle \left[0;\,\frac{\pi}{2}\right]\) кесіндідегі ең үлкен мәнге \(\displaystyle x=\frac{\pi}{3}{\small}\) нүктеде жеткенін білдіреді Оны есептейік:
\(\displaystyle f\left(\frac{\pi}{3}\right)=12\cos \frac{\pi}{3}+6\sqrt{3} \cdot\frac{\pi}{3}-2\sqrt{3}\pi +6=12\cdot\frac{1}{2}+\cancel{2\sqrt{3}\pi}-\cancel{2\sqrt{3}\pi} +6=12{\small.}\)
Жауабы: \(\displaystyle 12{\small.}\)

