Основания равнобедренной трапеции равны \(\displaystyle 8\) и \(\displaystyle 10\small,\) периметр равен \(\displaystyle 48\small.\) Найдите длину боковой стороны трапеции.
Воспользуемся определением равнобедренной трапеции.
Определение равнобедренной трапеции
Трапеция, у которой боковые стороны равны, называется равнобедренной.
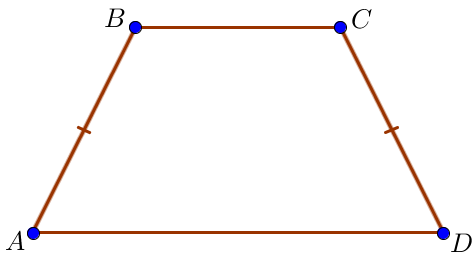
Пусть \(\displaystyle AB=CD=x\) – боковые стороны, \(\displaystyle \color{green}{BC}=\color{green}{8}\) и \(\displaystyle \color{red}{AD}=\color{red}{10}\) – основания равнобедренной трапеции. Периметр \(\displaystyle \color{blue}{P}\) многоугольника равен сумме длин всех его сторон. Тогда \(\displaystyle \color{blue}{P}=AB+\color{green}{BC}+CD+\color{red}{AD}\small.\)
| 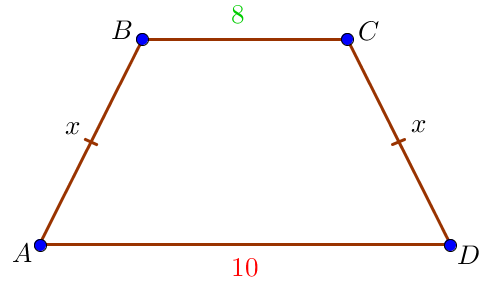 |
Значит,
\(\displaystyle \color{blue}{48}=x+\color{green}{8}+x+\color{red}{10}\small,\)
\(\displaystyle 48=18+2x\small,\)
откуда
\(\displaystyle 2x=48-18\small,\)
\(\displaystyle 2x=30\small,\)
\(\displaystyle x=15\small.\)
Ответ: \(\displaystyle 15{\small.}\)
