Решите неравенство
\(\displaystyle \left( 4^x-5\cdot 2^x \right)^2-20\left( 4^x-5\cdot 2^x \right) -96\leqslant 0{\small .}\)
\(\displaystyle \left( 4^x-5\cdot 2^x \right)^2-20\left( 4^x-5\cdot 2^x \right) -96\leqslant 0{\small .}\)
В левой части неравенства содержится выражение \(\displaystyle 4^x-5\cdot 2^x \) и его квадрат.
I. Сделаем замену переменной
\(\displaystyle \color{#336699}{a= 4^x-5\cdot 2^x {\small .}}\)
Получим квадратное неравенство:
\(\displaystyle \color{#336699}{a^2-20a-96\leqslant 0{\small .}}\)
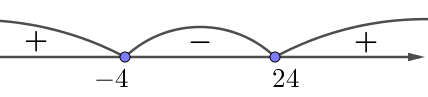
II. Решим полученное неравенство методом интервалов.
Получим:
\(\displaystyle \color{#336699}{-4\leqslant a \leqslant 24{\small .}}\)
III. Вернёмся к старой переменной.
У нас \(\displaystyle {a=4^x-5\cdot 2^x {\small .}}\)
Тогда
\(\displaystyle -4\leqslant 4^x-5\cdot 2^x \leqslant 24{\small .}\)
Получим систему неравенств:
\(\displaystyle \color{#336699}{\left\{\begin{array}{rl}t^2-5t-24& \leqslant \, 0{\small ,}\\t^2-5t+4&\geqslant\, 0{\small .}\\\end{array}\right.}\)
V. Решим полученную систему.
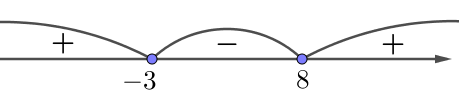
Решим каждое неравенство системы, потом найдём пересечение полученных множеств решений.
\(\displaystyle -3\leqslant t\leqslant 8\)
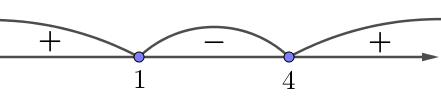
\(\displaystyle -\infty< t\leqslant 1{\small ;} \,\,\,\, 4 \leqslant t < +\infty\)
\(\displaystyle {-3\leqslant t\leqslant 1}{\small;}\) \(\displaystyle {4\leqslant t\leqslant 8{\small.}}\)
VI. Вернёмся к старой переменной.
Вернёмся к переменной \(\displaystyle x{\small .}\) У нас \(\displaystyle t=2^x{\small .}\)
Тогда:
\(\displaystyle \color{Blue}{-3\leqslant 2^x\leqslant 1}\) или \(\displaystyle \color{Blue}{4\leqslant 2^x\leqslant 8{\small.}}\)
Решим каждое неравенство.
Запишем двойное неравенство в виде системы неравенств:
\(\displaystyle \left\{\begin{array}{rcl}2^x& \geqslant-3,\\[5px]2^x& \leqslant \,1.\\\end{array}\right.\)
Решим каждое неравенство системы и найдём пересечение полученных множеств решений.
- Решим первое неравенство: \(\displaystyle 2^x \geqslant-3{\small .}\)
Показательная функция \(\displaystyle y=2^x\) принимает только положительные значения, поэтому неравенство \(\displaystyle {2^x \geqslant-3}{\small}\) выполняется при любых действительных значениях переменной \(\displaystyle x{\small .}\)
То есть, решением первого неравенства является промежуток \(\displaystyle (-\infty;+\infty){\small .}\)
- Решим второе неравенство: \(\displaystyle 2^x \leqslant 1{\small .}\)
\(\displaystyle 2^x \leqslant 1\Leftrightarrow 2^x \leqslant 2^0{\small .}\)
Так как основание степени \(\displaystyle 2>1{\small,}\) то при переходе к неравенству на показатели знак неравенства не изменится.
Получим: \(\displaystyle x \leqslant 0{\small. } \)
То есть, решением данного неравенства является промежуток \(\displaystyle (-\infty;0]{\small .}\)
- Пересечением полученных промежутков \(\displaystyle (-\infty;+\infty)\) и \(\displaystyle (-\infty;0]\) является \(\displaystyle (-\infty;0]{\small .}\)
Запишем двойное неравенство в виде системы неравенств:
\(\displaystyle \left\{\begin{array}{rcl}2^x& \geqslant4,\\[5px]2^x& \leqslant \,8.\\\end{array}\right.\Leftrightarrow\left\{\begin{array}{rcl}2^x& \geqslant2^2,\\[5px]2^x& \leqslant \,2^3.\\\end{array}\right.\)
Так как основание степени \(\displaystyle 2>1{\small,}\) то при переходе к неравенствам на показатели знаки неравенств не изменятся.
Получим:
\(\displaystyle\left\{\begin{array}{rcl}x& \geqslant2,\\[5px]x& \leqslant \,3.\\\end{array}\right.\)
То есть, решением данного двойного неравенства является промежуток \(\displaystyle [2;3]{\small .}\)
Решением исходного неравенства является объединение найденных промежутков:
\(\displaystyle \color{Blue}{(-\infty ;0] \cup [2;3]{\small. }} \)
Ответ: \(\displaystyle x\in (-\infty ;0]{\small } \cup [2;3]{\small. } \)