Екі түзудің қиылысуынан пайда болған бұрыштардың бірі екіншісінен \(\displaystyle 5\) есе үлкен. Үлкен бұрыш қанша градусты құрайды?
\(\displaystyle ^{\circ}\)
Іргелес және тік бұрыштар. Іргелес және тік бұрыштардың қасиеттері
\(\displaystyle ABC\) жазыңқы бұрышының ішінде \(\displaystyle BD\) сәулесі жүргізілген. Ол жазыңқы бұрышты іргелес бұрыштар деп аталатын екі бұрыш - \(\displaystyle ABD\) және \(\displaystyle DBC\) бөледі.
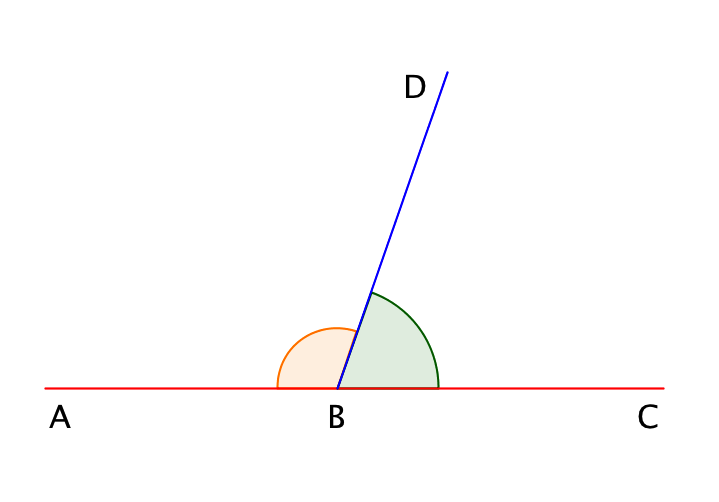
Іргелес бұрыштардың қосындысы \(\displaystyle 180\) градусқа тең:
\(\displaystyle ∠ ABD+∠ DBC=180^{\circ}.\)
Егер екі \(\displaystyle AB\) және \(\displaystyle CD\) түзулері \(\displaystyle O\) нүктесінде қиылысса, онда \(\displaystyle AOC\) және \(\displaystyle BOD\) бұрыштары тік деп аталады. Тік бұрыштардың басқа жұбы \(\displaystyle AOD\) және \(\displaystyle BOC\) бұрыштары болып табылады:
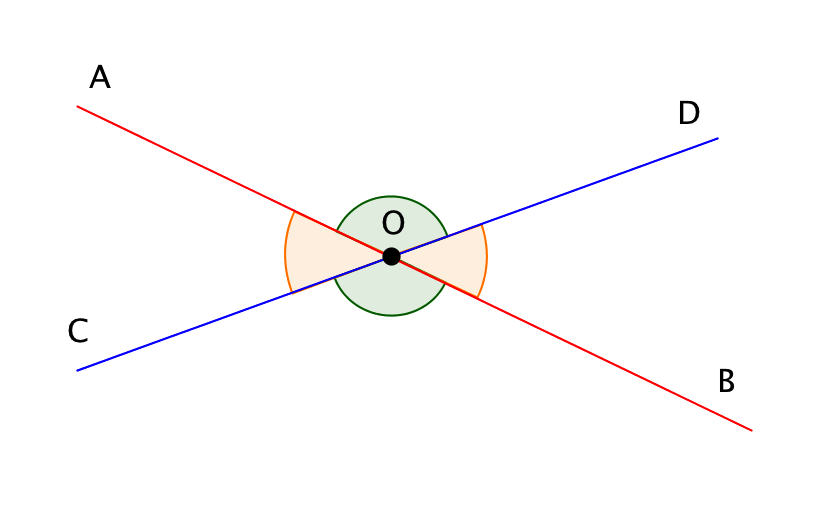
Тік бұрыштар келесіге тең:
\(\displaystyle ∠ AOC=∠ BOD,\)
\(\displaystyle ∠ AOD=∠ BOC.\)
\(\displaystyle AB\) және \(\displaystyle CD\) түзулері \(\displaystyle O\) нүктесінде қиылыссын . Бұл жағдайда төрт бұрыш – \(\displaystyle ∠ AOD\), \(\displaystyle ∠ BOD\), \(\displaystyle ∠ BOC\), \(\displaystyle ∠ AOC\) пайда болады:
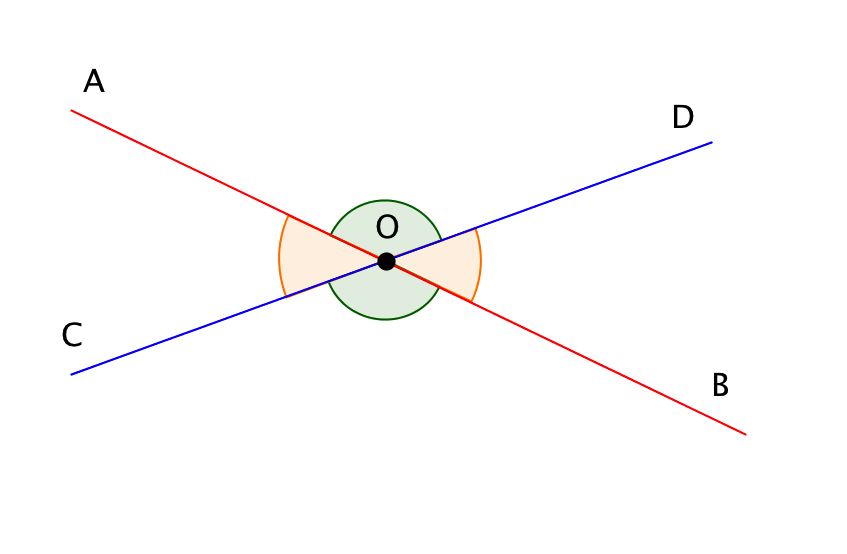
Есеп шартына сәйкес бұрыштардың бірі екіншісінен \(\displaystyle 5\) есе үлкен. Тік бұрыштар келесіге тең болғандықтан, шартта қарастырылған бұрыштар тек іргелес болуы мүмкін. Сондықтан, есепті шешу үшін кез-келген екі іргелес бұрышты таңдайық – мысалы, \(\displaystyle ∠ AOD\) мен \(\displaystyle ∠ AOC\) , және \(\displaystyle ∠ AOD\) неге тең екенін табайық.
Шарт бойынша, \(\displaystyle ∠ AOD\) \(\displaystyle ∠ AOC\)-тен \(\displaystyle 5\) есе үлкен, яғни
\(\displaystyle ∠ AOD=5 \cdot ∠ AOC.\)
\(\displaystyle ∠ AOC\) және \(\displaystyle ∠ AOD\) іргелес болғандықтан, онда
\(\displaystyle ∠ AOC + ∠ AOD=180^{\circ}.\)
Сонда
\(\displaystyle ∠ AOC + 5 \cdot ∠ AOC=180^{\circ},\)
\(\displaystyle 6 \cdot ∠ AOC=180^{\circ},\)
\(\displaystyle ∠ AOC=\frac{180^{\circ}}{6}=30^{\circ},\)
\(\displaystyle ∠ AOD=5\cdot 30^{\circ}=150^{\circ}.\)
Жауабы: \(\displaystyle 150^{\circ}.\)
