\(\displaystyle AB\), \(\displaystyle CD\) және \(\displaystyle EF\) түзулерінің \(\displaystyle O\) нүктесінде қиылысуында үш жұп тік бұрыш пайда болды. \(\displaystyle ∠ AOC\) \(\displaystyle ∠ COE\)-ден \(\displaystyle 3\) есе үлкен, ал \(\displaystyle ∠ AOF\) \(\displaystyle ∠ COE\)-ден \(\displaystyle 80^{\circ}\) үлкен екендігі белгілі. \(\displaystyle ∠ COE\), \(\displaystyle ∠ AOC\) және \(\displaystyle ∠ AOF\) шамаларын анықтаңыз.
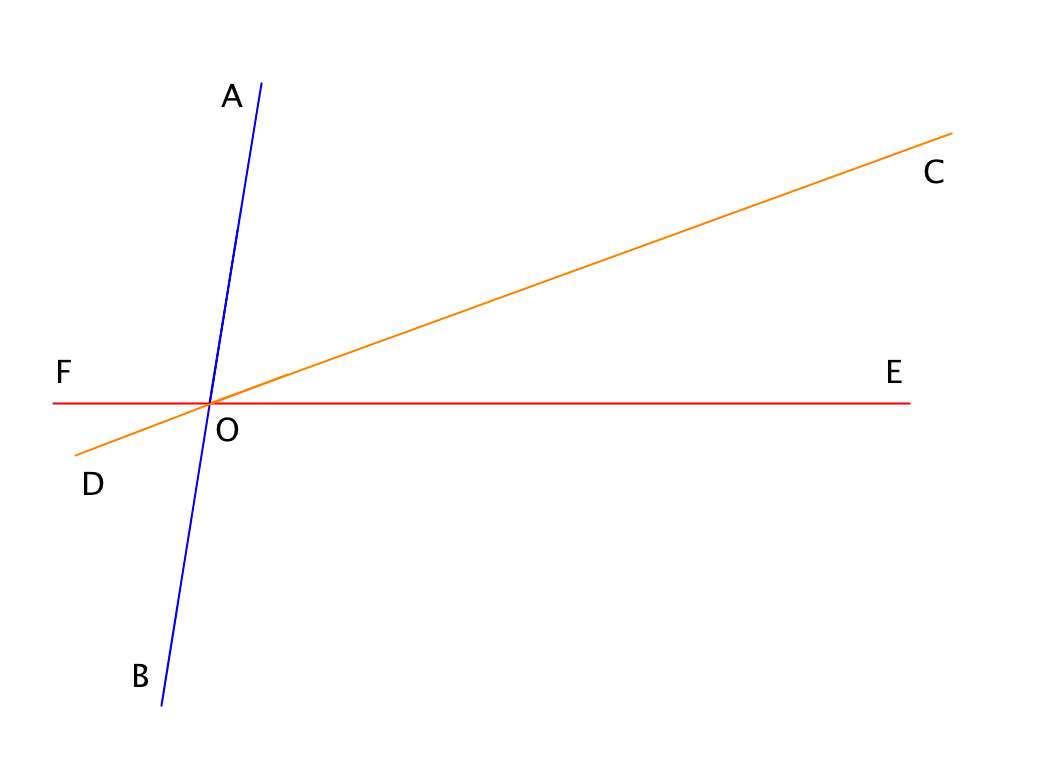
\(\displaystyle ∠ COE=\)\(\displaystyle ^{\circ}\);
\(\displaystyle ∠ AOC=\)\(\displaystyle ^{\circ}\);
\(\displaystyle ∠ AOF=\)\(\displaystyle ^{\circ}\)
Іргелес және тік бұрыштар. Іргелес және тік бұрыштардың қасиеттері
\(\displaystyle ABC\) жазыңқы бұрышының ішінде \(\displaystyle BD\) сәулесі жүргізілген. Ол жазыңқы бұрышты іргелес бұрыштар деп аталатын екі бұрыш - \(\displaystyle ABD\) және \(\displaystyle DBC\) бөледі.
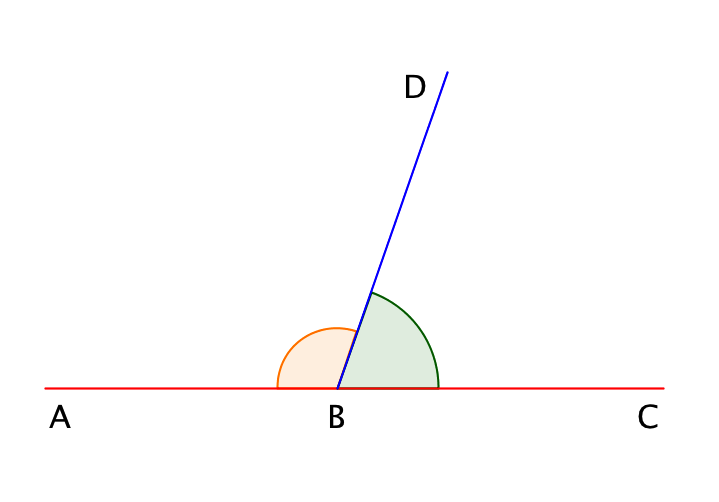
Іргелес бұрыштардың қосындысы \(\displaystyle 180\) градусқа тең:
\(\displaystyle ∠ ABD+∠ DBC=180^{\circ}.\)
Егер екі \(\displaystyle AB\) және \(\displaystyle CD\) түзулері \(\displaystyle O\) нүктесінде қиылысса, онда \(\displaystyle AOC\) және \(\displaystyle BOD\) бұрыштары тік деп аталады. Тік бұрыштардың басқа жұбы \(\displaystyle AOD\) және \(\displaystyle BOC\) бұрыштары болып табылады:
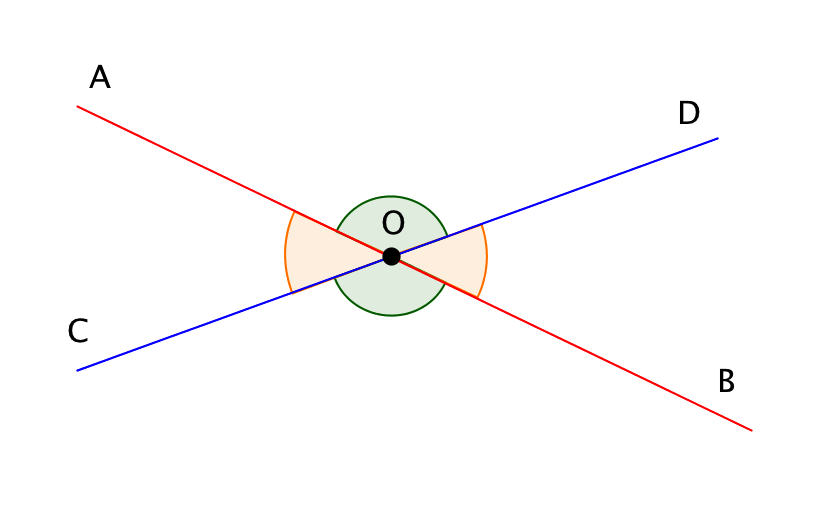
Тік бұрыштар келесіге тең:
\(\displaystyle ∠ AOC=∠ BOD,\)
\(\displaystyle ∠ AOD=∠ BOC.\)
\(\displaystyle AB\), \(\displaystyle CD\) және \(\displaystyle EF\) түзулерінің \(\displaystyle O\) нүктесінде қиылысуында үш жұп тік бұрыш пайда болады:
- \(\displaystyle ∠ AOF\) және \(\displaystyle ∠ BOE\);
- \(\displaystyle ∠ DOF\) және \(\displaystyle ∠ COE\);
- \(\displaystyle ∠ BOD\) және \(\displaystyle ∠ AOC\).
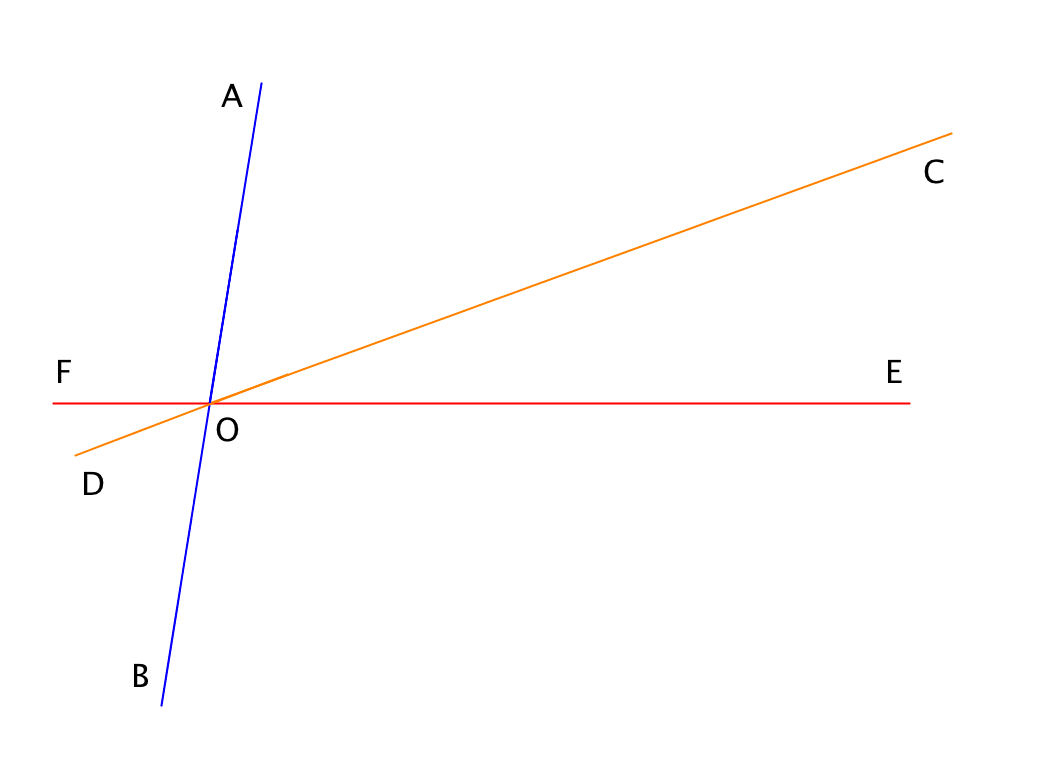
Бұл ретте
\(\displaystyle ∠ AOF=∠ BOE,\)
\(\displaystyle ∠ DOF=∠ COE,\)
\(\displaystyle ∠ BOD=∠ AOC.\)
Тік бұрыштардың әр жұбынан олардың қосындысы жазыңқы бұрыш құрайтындай етіп бір бұрыштан алайық. Мысалы,
\(\displaystyle ∠ EOF=∠ COE+∠ AOC+∠ AOF=180^{\circ}.\)
Шартқа сәйкес, \(\displaystyle ∠ AOC\) \(\displaystyle ∠ COE\)-ден \(\displaystyle 3\) есе үлкен, яғни
\(\displaystyle ∠ AOC=3 \cdot ∠ COE.\)
Сондай-ақ, шартқа сәйкес, \(\displaystyle ∠ AOF\) \(\displaystyle ∠ COE\)-ден \(\displaystyle 80^{\circ}\) үлкен, яғни
\(\displaystyle ∠ AOF=∠ COE+80^{\circ}.\)
Сонда,
\(\displaystyle 180^{\circ}=∠ COE+3 \cdot ∠ COE+(∠ COE+80^{\circ}),\)
\(\displaystyle 5 \cdot ∠ COE=180^{\circ}-80^{\circ}=100^{\circ},\)
\(\displaystyle ∠ COE=\frac{100^{\circ}}{5}=20^{\circ}.\)
Демек,
\(\displaystyle ∠ AOC=3 \cdot ∠ COE=3 \cdot 20^{\circ}=60^{\circ},\)
\(\displaystyle ∠ AOF=∠ COE+80^{\circ}=20^{\circ}+80^{\circ}=100^{\circ}.\)
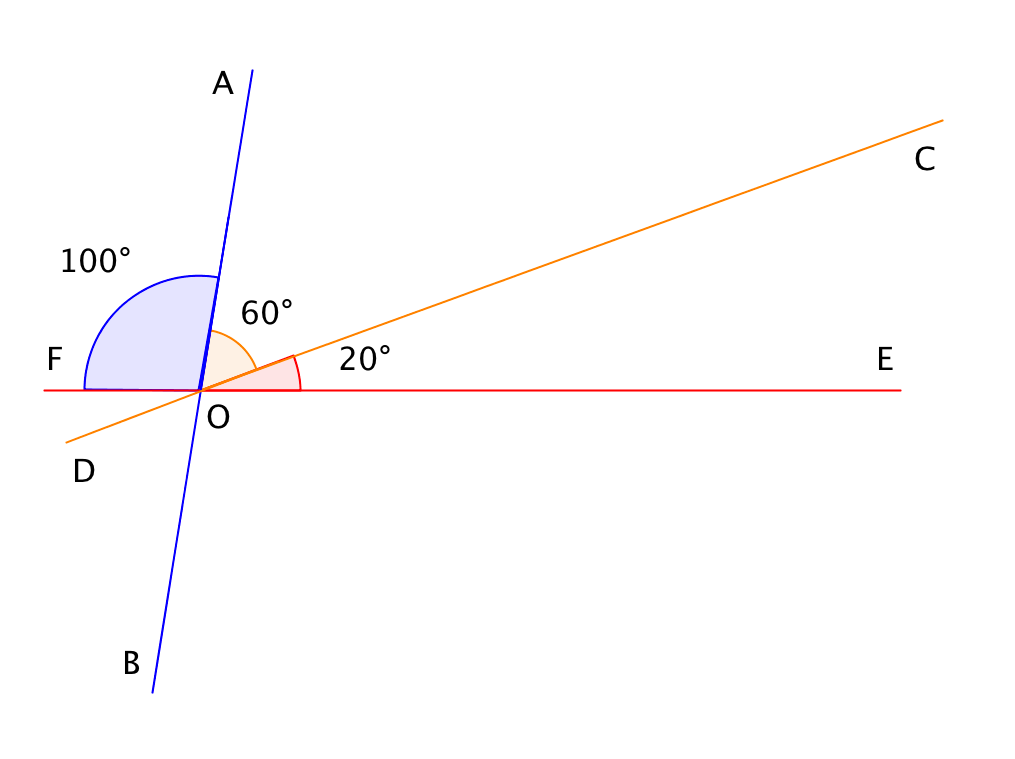
Келесі тексеруді орындайық:
\(\displaystyle ∠ EOF=∠ COE + ∠ AOC + ∠ AOF= 20^{\circ} + 60^{\circ} + 100^{\circ} = 180^{\circ}.\)
Жауабы: \(\displaystyle ∠ COE=20^{\circ}\); \(\displaystyle ∠ AOC=60^{\circ}\); \(\displaystyle ∠ AOF=100^{\circ}\).
