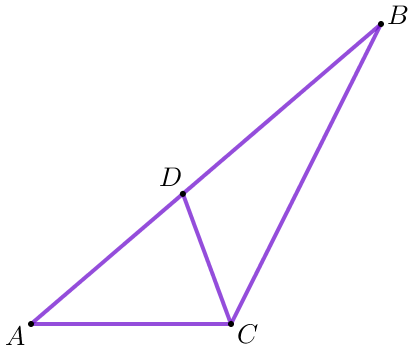
Точка \(\displaystyle D\) на стороне \(\displaystyle AB\) треугольника \(\displaystyle ABC\) выбрана так, что \(\displaystyle AD=AC {\small.}\) Известно, что \(\displaystyle \angle ACB=124^{\circ}\) и \(\displaystyle \angle CAB=39^{\circ} {\small.}\) Найдите \(\displaystyle \angle DCB {\small.}\) Ответ дайте в градусах.
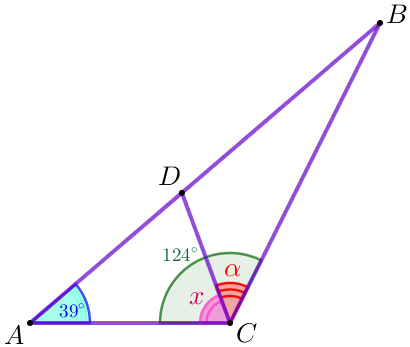 | Пусть \(\displaystyle \angle DCB=\color{red} { \alpha} {\small,}\) \(\displaystyle \angle ACD=\color{Magenta}x{\small.}\) По рисунку \(\displaystyle \color{red} { \alpha} = 124^ {\circ}- \color{Magenta}x{\small.}\) |
Так как треугольник \(\displaystyle ACD\) – равнобедренный, то \(\displaystyle \angle ADC=\angle ACD=\color{Magenta}x{\small.}\) Сумма углов в треугольнике равна \(\displaystyle 180 ^{\circ} {\small . } \) Тогда \(\displaystyle \color{Magenta}{x}+ \color{Magenta}{x}+39^{\circ}= 180^\circ{\small , } \) \(\displaystyle 2 \cdot \color{Magenta}{x}= 180^\circ - 39^{\circ}{\small , } \) \(\displaystyle \color{Magenta}{x}= \frac{1}{2} \cdot 141^\circ=70{,}5^{\circ}{\small . } \) | 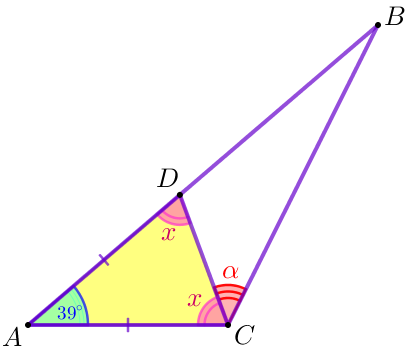 |
Получаем
\(\displaystyle \color{red} { \alpha} = 124^{\circ}- \color{Magenta}x=124^{\circ}-70{,}5^{\circ}=53{,}5^{\circ}{\small.}\)
Таким образом, \(\displaystyle \angle DCB=53{,}5^{\circ}{\small.}\)
Ответ: \(\displaystyle 53{,}5 {\small.}\)
