Трапецияның табандары \(\displaystyle 4\) және \(\displaystyle 10\) тең . Оның диагональдарының бірі осы трапецияның орта сызығын бөлетін кесінділердің ең үлкенін табыңыз.
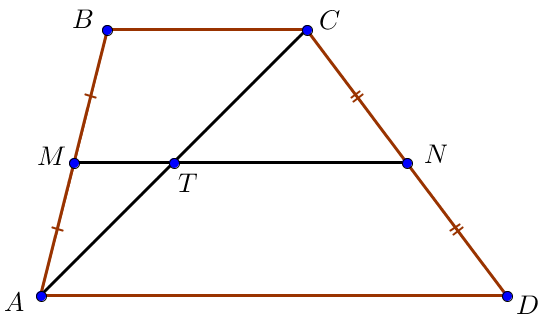
\(\displaystyle BC=4\) және \(\displaystyle AD=10\) – табандары, \(\displaystyle M\) және \(\displaystyle N\) – трапецияның \(\displaystyle AB\) және \(\displaystyle CD\small\) бүйір қабырғаларының ортаңғы нүктелері болсын. Сонда \(\displaystyle MN\) – трапецияның орта сызығы.
\(\displaystyle AC\small\) диагональін сызамыз, оның орта түзуімен қиылысу нүктесі \(\displaystyle T\) – болсын.
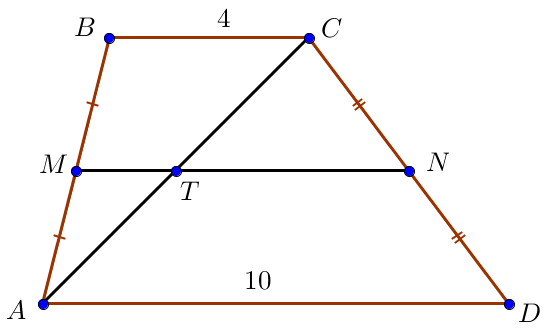
Трапецияның орта сызығының қасиеті бойынша \(\displaystyle MN\) түзуі \(\displaystyle AD\) және \(\displaystyle BC\small\) түзулеріне параллель
\(\displaystyle ACD\) үшбұрышында \(\displaystyle TN\) кесіндісі \(\displaystyle AD\) қабырғасына параллель және \(\displaystyle CD\small\) қабырғасының ортасынан өтеді.
Фалес теоремасының салдарын қолданамыз.
Фалес теоремасының салдары
Үшбұрыштың екінші қабырғасына параллель қабырғасының ортасы арқылы өтетін түзу үшбұрыштың үшінші қабырғасын екіге бөледі.
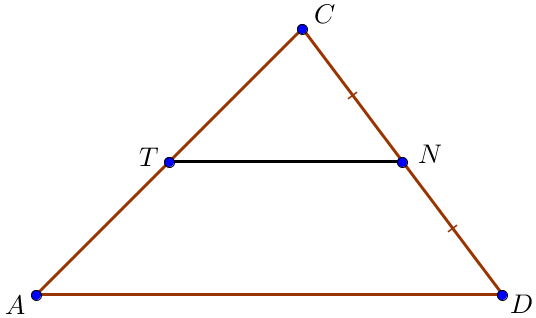
Егер \(\displaystyle CN=ND\) және \(\displaystyle TN\parallel AD\small,\) болса, онда \(\displaystyle AT=TC\small.\)
Фалес теоремасының салдары бойынша \(\displaystyle AT=TC\small,\) мұндағы \(\displaystyle T\) – \(\displaystyle AC\small\) нүктесінің ортасы
Сонда \(\displaystyle TN\) – \(\displaystyle ACD\small\) үшбұрышының орта сызығы және \(\displaystyle TM\) – \(\displaystyle ACB\small\) үшбұрышының орта сызығы
Үшбұрыштың орта сызығының қасиеті бойынша
\(\displaystyle TN=\frac{1}{2} AD =\frac{1}{2} \cdot 10 = 5\)
және
\(\displaystyle TM=\frac{1}{2} BC =\frac{1}{2} \cdot 4 = 2\small.\)
Демек, \(\displaystyle TN\) – \(\displaystyle AC\small\) диагональінің трапецияның орта сызығын бөлетін кесінділердің ең үлкені
Жауабы: \(\displaystyle 5{\small .}\)
Есепті шешу барысында трапецияның орта сызығының келесі қасиетін алдық:
Трапецияның орта сызығының қасиеті
Трапецияның ортаңғы сызығы трапеция диагональдарының ортаңғы нүктелері арқылы өтеді:
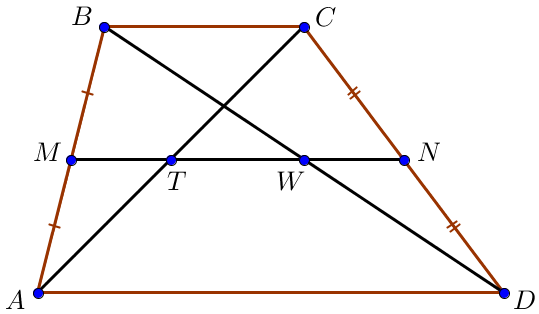
\(\displaystyle T\) және \(\displaystyle W\) – нүктелері \(\displaystyle AC\) және \(\displaystyle BD\small\) диагональдарының ортаңғы нүктелері болып табылады
