Основания трапеции равны \(\displaystyle 4\) и \(\displaystyle 10\small.\) Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
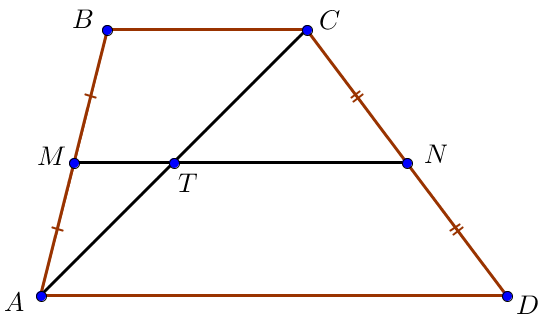
Пусть \(\displaystyle BC=4\) и \(\displaystyle AD=10\) – основания, \(\displaystyle M\) и \(\displaystyle N\) – середины боковых сторон \(\displaystyle AB\) и \(\displaystyle CD\small.\) Тогда \(\displaystyle MN\) – средняя линия трапеции.
Проведем диагональ \(\displaystyle AC\small,\) пусть \(\displaystyle T\) – точка ее пересечения со средней линией.
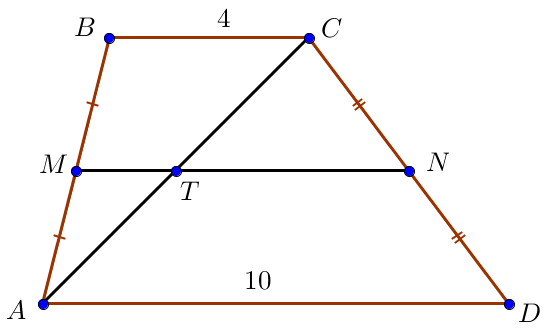
По свойству средней линии трапеции прямая \(\displaystyle MN\) параллельна прямым \(\displaystyle AD\) и \(\displaystyle BC\small.\)
В треугольнике \(\displaystyle ACD\) отрезок \(\displaystyle TN\) параллелен стороне \(\displaystyle AD\) и проходит через середину стороны \(\displaystyle CD\small.\)
Воспользуемся следствием теоремы Фалеса.
Следствие теоремы Фалеса
Прямая, проходящая через середину стороны треугольника параллельно другой стороне, делит третью сторону треугольника пополам.
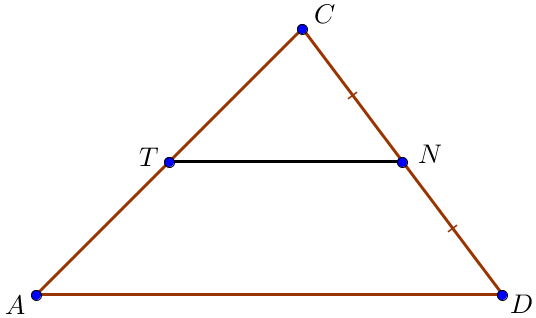
Если \(\displaystyle CN=ND\) и \(\displaystyle TN\parallel AD\small,\) то \(\displaystyle AT=TC\small.\)
По следствию теоремы Фалеса \(\displaystyle AT=TC\small,\) откуда \(\displaystyle T\) – середина \(\displaystyle AC\small.\)
Тогда \(\displaystyle TN\) – средняя линиия треугольника \(\displaystyle ACD\small,\) и \(\displaystyle TM\) – средняя линия треугольника \(\displaystyle ACB\small.\)
По свойству средней линии треугольника
\(\displaystyle TN=\frac{1}{2} AD =\frac{1}{2} \cdot 10 = 5\)
и
\(\displaystyle TM=\frac{1}{2} BC =\frac{1}{2} \cdot 4 = 2\small.\)
Значит, \(\displaystyle TN\) – больший из отрезков, на которые делит среднюю линию трапеции диагональ \(\displaystyle AC\small.\)
Ответ: \(\displaystyle 5{\small .}\)
В ходе решения задачи мы получили следующее свойство средней линии трапеции:
Свойство средней линии трапеции
Средняя линия трапеции проходит через середины диагоналей трапеции:
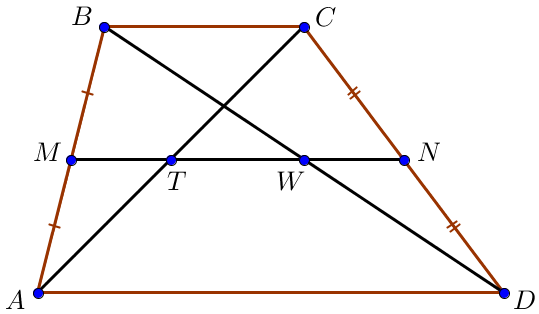
точки \(\displaystyle T\) и \(\displaystyle W\) – середины диагоналей \(\displaystyle AC\) и \(\displaystyle BD\small.\)
