\(\displaystyle A\ - \) "бірінші рет көк фломастер үшінші алғаннан пайда болды" оқиғасы болсын.  

Мүмкін болатын нәтижелердің графигін құруды бастайық:

• қызыл көрсеткімен біз "қораптан қызыл фломастер шығарылды" қарапайым оқиғасын белгілейміз,
• көк көрсеткімен біз "қораптан көк фломастер шығарылды" қарапайым оқиғасын белгілейміз.      

Қарапайым оқиғалардың ықтималдығын классикалық ықтималдық формуласы бойынша есептейміз.

Тапсырманың шарты бойынша ең бірінші қызыл фломастерді шығару керек.

Жалпы фломастерлер саны \(\displaystyle 6\), оның ішінде \(\displaystyle 4\) фломастерлер қызыл болғандықтан, бұл оқиға \(\displaystyle \frac{4}{6}\small\) ықтималдықпен болады.         

Біз қолайлы тармақ бойынша ықтимал нәтижелердің графигін құруды жалғастырамыз және онда қолайлы оқиғаның табылған ықтималдығын белгілейміз.

Екінші қадамда тағы да қызыл фломастерді шығару керек. 

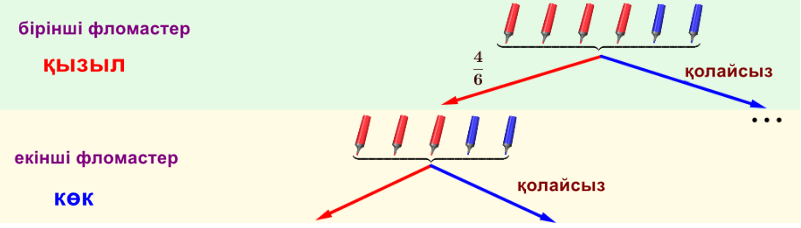
Бірінші қадамда қызыл фломастер шығарылғаннан кейін барлығы \(\displaystyle 5\) фломастер қалды, оның ішінде \(\displaystyle 3\) қызыл. Сонымен, екінші қадамда қызыл фломастерді шығару ықтималдығы \(\displaystyle \frac{3}{5} \small.\)      

Біз қолайлы тармақ бойынша ықтимал нәтижелердің графигін құруды жалғастырамыз және онда қолайлы оқиғаның табылған ықтималдығын белгілейміз.

Үшінші қадамда бізге көк фломастерді шығару керек.   

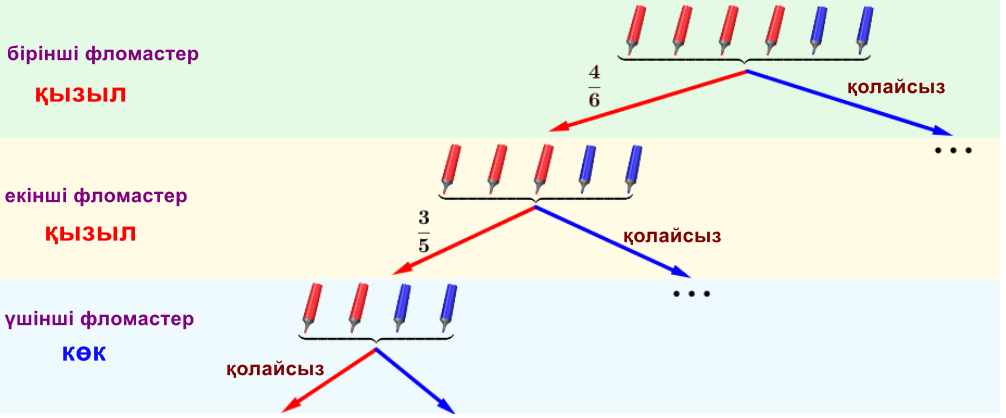
\(\displaystyle 4\) фломастер қалды, оның ішінде \(\displaystyle 2\) көк. Демек, үшінші қадамда көк фломастерді шығару ықтималдығы \(\displaystyle \frac{2}{4}\small\) тең болады.               

Біз бағанда табылған ықтималдықты белгілейміз және түсінікті болу үшін қолайсыз нәтижелерге сәйкес келетін көрсеткілерді алып тастаймыз.

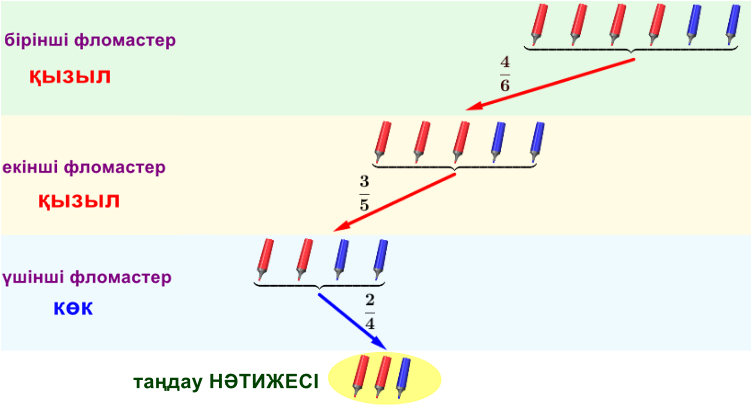
\(\displaystyle A\) оқиғасы бағандағы жалғыз жолға сәйкес келеді.   

Үш қолайлы қиылыспайтын нәтижелердің бір уақытта пайда болу ықтималдығы олардың ықтималдықтарының көбейтіндісіне тең. 

Демек,

\(\displaystyle P(A)=\frac{4}{6} \cdot \frac{3}{5} \cdot \frac{2}{4}=\frac{1}{5}=0{,}2.\)

Жауабы: \(\displaystyle 0{,}2.\)