\(\displaystyle y=x^2\) параболасын солға \(\displaystyle 3\) бірлікке жылжытқанда (\(\displaystyle \rm OX\) осі бойымен) алынған параболаның теңдеуін жазыңыз.
\(\displaystyle y=(x\)\(\displaystyle )^{\,2}\)
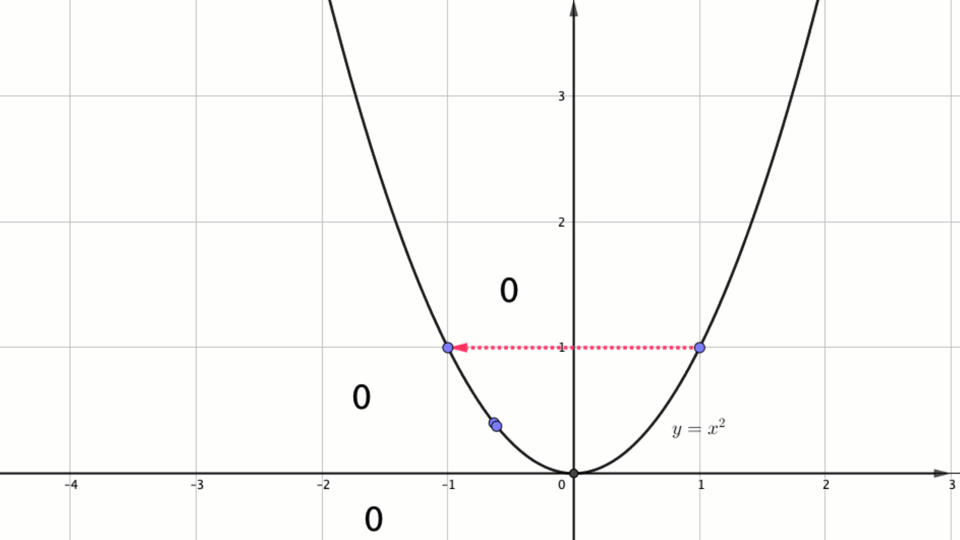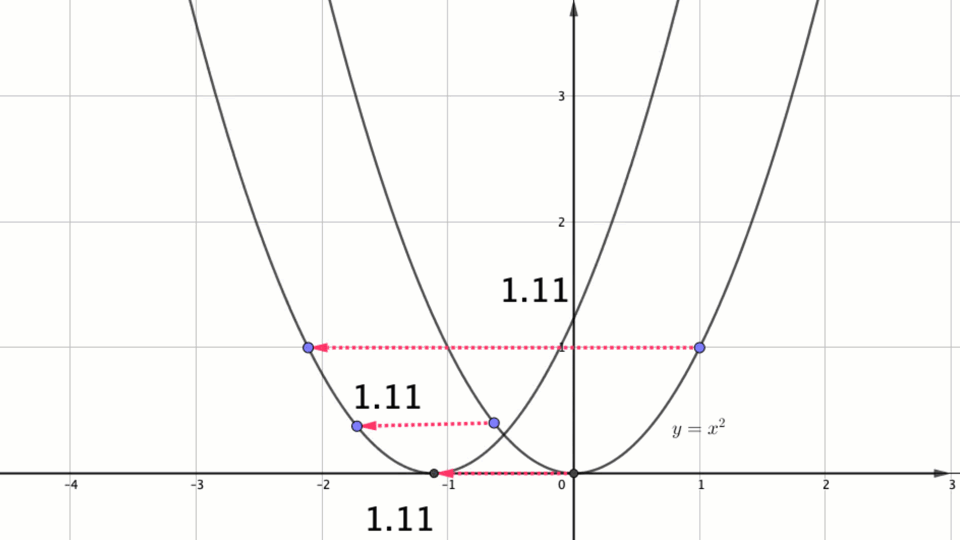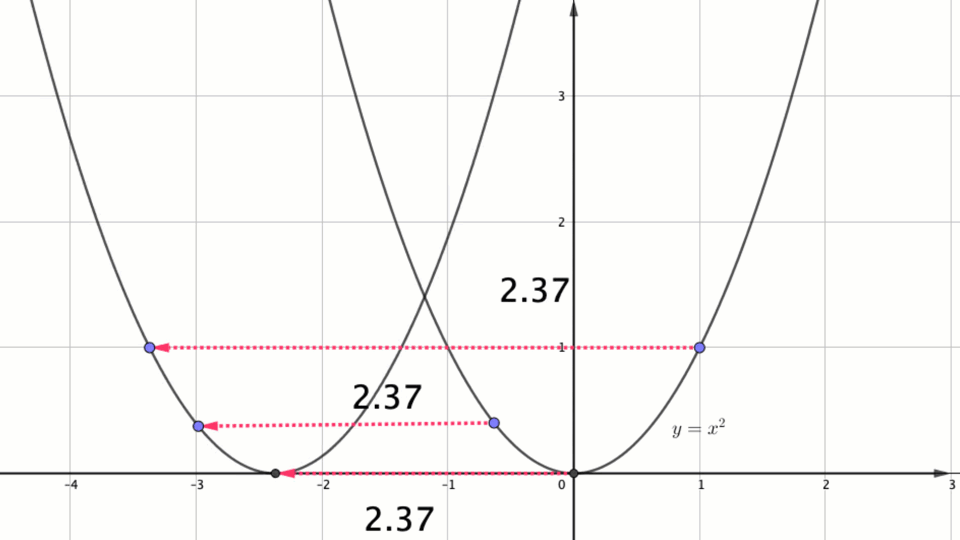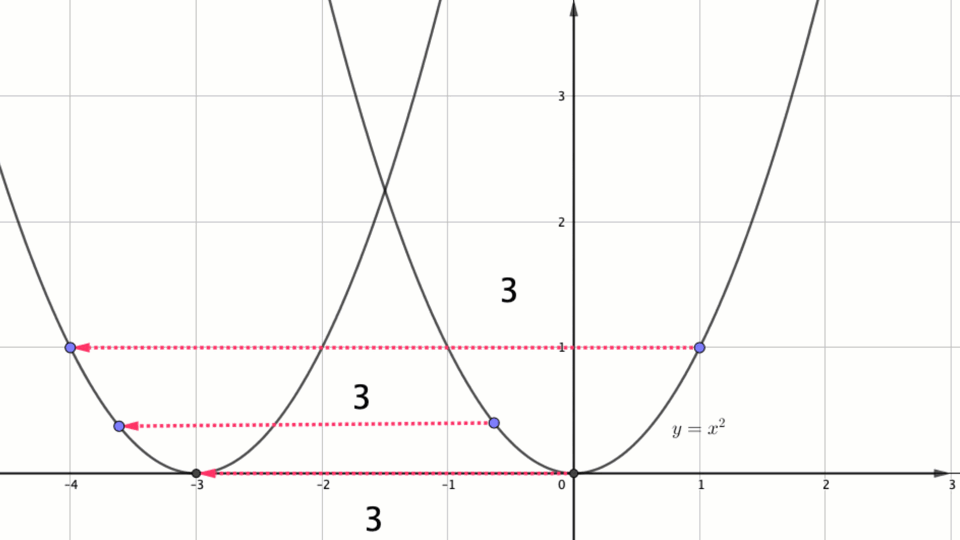
Егер координаталары \(\displaystyle (x_0\,; y_0)\) болатын кейбір нүкте ось бойымен \(\displaystyle a\) бірлікке солға жылжытылса \(\displaystyle \rm OX\), онда \(\displaystyle (x_0- a\,; y_0){\small }\) координаталары бар нүктені аламыз
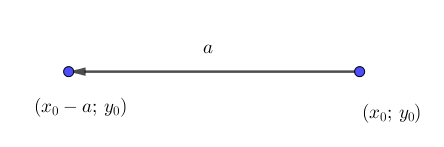
Егер
\(\displaystyle x^{\prime}=x_0-\color{red}{a}\) және \(\displaystyle y^{\prime}=y_0{\small .}\)
Онда
\(\displaystyle \color{blue}{x_0}=\color{blue}{x^{\prime}+ \color{red}{a}}\) және \(\displaystyle \color{green}{y_0}=\color{green}{y^{\prime}}{\small .}\)
Демек, \(\displaystyle \color{green}{y_0}=f(\color{blue}{x_0})\) ішінде \(\displaystyle \color{blue}{x_0}\) орнына \(\displaystyle \color{blue}{x^{\prime}}+ \color{red}{a}\) және \(\displaystyle \color{green}{y_0}\) \(\displaystyle \color{green}{y^{\prime}}{ \small ,}\) ауыстырсақ, онда аламыз.
\(\displaystyle \color{green}{y^{\prime}}=f(\color{blue}{x^{\prime}}+ \color{red}{a}){\small .}\)
Осылайша,
әрбір нүкте бірлікті ось бойымен солға жылжытқаннан кейін \(\displaystyle \rm OX\) теңдеуді қанағаттандырады
\(\displaystyle y=f(x+\color{red}{a}){\small .}\)
Ережені құрастыруға болады.
Егер \(\displaystyle y=x^2 \) функциясының графигі ось бойымен \(\displaystyle \color{red}{a}\) бірлікке солға жылжытылса \(\displaystyle \rm OX{\small ,}\) онда функцияның графигі болады
\(\displaystyle y=(x+\color{red}{a})^2{\small .} \)
Есептің шарты бойынша парабола \(\displaystyle y=x^2\) ось бойымен \(\displaystyle \rm OX{\small }\) солға \(\displaystyle 3\) бірлікке ығысқан.
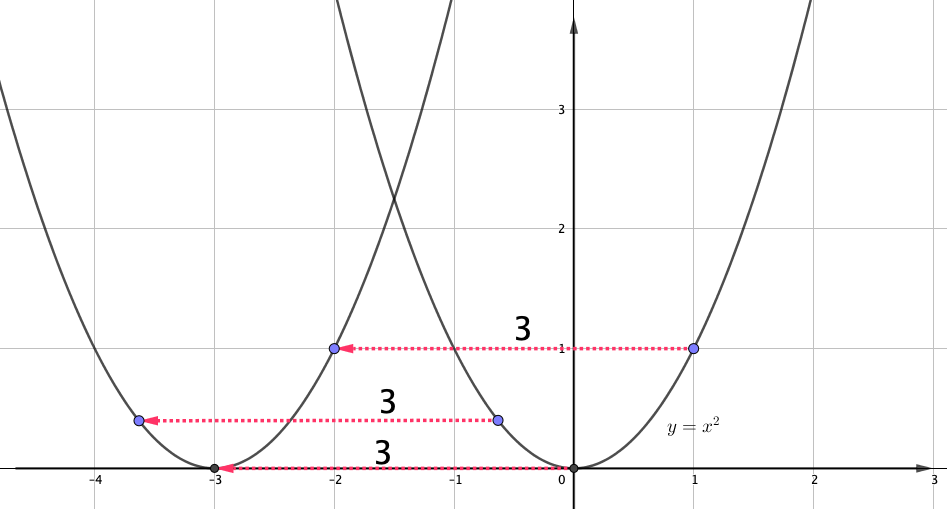
Содан кейін ереже бойынша функцияның графигін аламыз
\(\displaystyle y= (x+3)^2{\small . }\)
Жауабы:\(\displaystyle y= (x+3)^2{\small . }\)
