Бұл теңсіздік үшін
\(\displaystyle \frac{x+2}{x-1} \ge 0\)
берілген аралықтар бойынша өрнекпен қабылданған белгілерді көрсетіңіз.
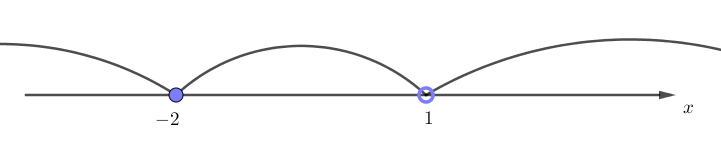
\(\displaystyle f(x)=\frac{x+2}{x-1}{\small } \) деп белгілеңіз. \(\displaystyle f(x) \) функциясының сәйкес аралықтардағы белгілерін анықтаңыз.
Функцияның аралықтағы таңбасын табу үшін осы аралықтан айнымалының ерікті мәнін алып, оны функцияның орнына қоямыз.
\(\displaystyle f(x)=\frac{x+2}{x-1}\) функциясы үшін осы аралықтар мен осы аралықтағы айнымалының мәнін ретімен салыстырайық.
| Аралық | Аралықтағы сан | Функцияның аралықтағы мәні |
| \(\displaystyle (-\infty;-2) \) | \(\displaystyle x=-3 \) | \(\displaystyle f(-3) \) |
| \(\displaystyle (-2;1) \) | \(\displaystyle x=0 \) | \(\displaystyle f(0) \) |
| \(\displaystyle (1;+\infty) \) | \(\displaystyle x=2 \) | \(\displaystyle f(2) \) |
Алынған аралықтардағы функцияның таңбаларын табайық.
\(\displaystyle f(-3)\) функциясының мәнін табыңыз.
\(\displaystyle f(\color{red}{ x})=\frac{\color{red}{ x}+2}{\color{red}{ x}-1}{ \small .} \)
ауыстыру \(\displaystyle \color{red}{ x}=-3{\small : }\)
\(\displaystyle f(\color{red}{ -3})=\frac{\color{red}{ -3}+2}{\color{red}{ -3}-1}{ \small ,} \)
\(\displaystyle f(-3)=\frac{ 1}{ 4 }{\small .} \)
Сонымен, \(\displaystyle f(-3)>0{\small .} \)
Сондықтан, \(\displaystyle (-\infty;-2) \) аралығында функция оң болады және \(\displaystyle +{\small }\) таңбасын жазамыз.
\(\displaystyle f(0)\) функциясының мәнін табыңыз.
\(\displaystyle f(\color{red}{ x})=\frac{\color{red}{ x}+2}{\color{red}{ x}-1}{ \small .} \)
ауыстыру \(\displaystyle \color{red}{ x}=0{\small : }\)
\(\displaystyle f(\color{red}{ 0})=\frac{\color{red}{ 0}+2}{\color{red}{ 0}-1}{ \small ,} \)
\(\displaystyle f(0)=-2{\small .} \)
Сонымен, \(\displaystyle f(0)<0{\small .} \)
Сондықтан, \(\displaystyle (-2;1) \) аралығында функция теріс болады және \(\displaystyle -{\small }\) таңбасын жазамыз.
\(\displaystyle f(2)\) функциясының мәнін табыңыз.
\(\displaystyle f(\color{red}{ x})=\frac{\color{red}{ x}+2}{\color{red}{ x}-1}{ \small .} \)
ауыстыру \(\displaystyle \color{red}{ x}=2{\small : }\)
\(\displaystyle f(\color{red}{ 2})=\frac{\color{red}{ 2}+2}{\color{red}{ 2}-1}{ \small ,} \)
\(\displaystyle f(2)=4{\small .} \)
Сонымен, \(\displaystyle f(2)>0{\small .} \)
Сондықтан \(\displaystyle (1;+\infty) \) аралығында функция оң болады және \(\displaystyle +{\small }\) таңбасын жазамыз.
Осылайша,
