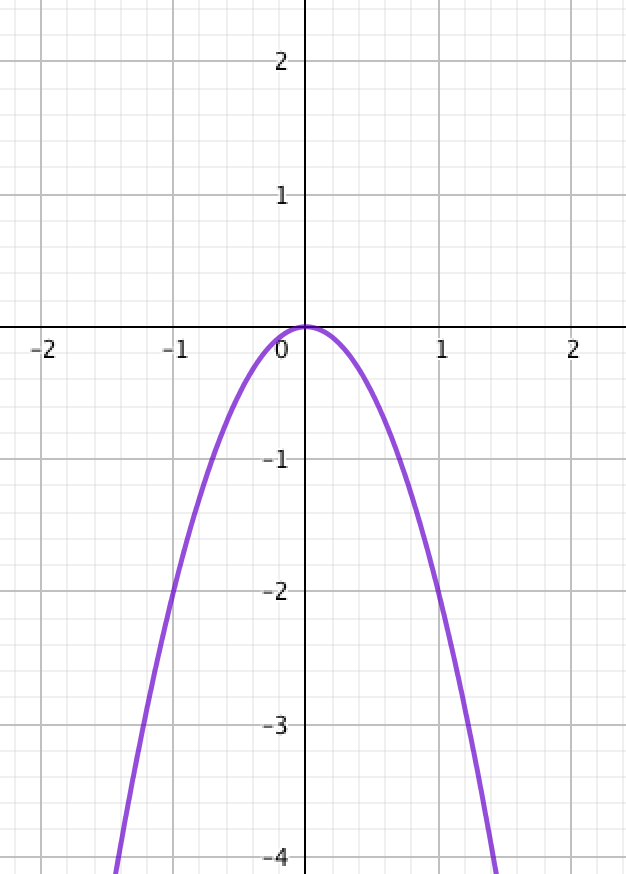
\(\displaystyle y=ax^2{\small }\) квадраттық функциясының графигі бойынша \(\displaystyle a\) коэффициентінің таңбасын анықтаңыз.
\(\displaystyle a\)\(\displaystyle 0\)
Анықтаманы қолданайық.
Функция графигі
Жазықтықтағы \(\displaystyle y=\color{blue}{f(x)}\) функциясының графигі
\(\displaystyle \{(x;\, \color{blue}{f(x)})| \, x\) анықтау аймағына жатады \(\displaystyle \}{\small }\) нүктелерінің жиыны деп аталады.
\(\displaystyle y=ax^2\) параболасының графигі барлық нақты \(\displaystyle x{\small }\)сандары үшін \(\displaystyle \{(x;\, ax^2) \}\) түрінің нүктелер жиыны болып табылады.
Параболаның барлық нүктелері \(\displaystyle \rm OX{ \small }\) осінен төмен орналасқандықтан, онда барлық нөлдік емес нақты \(\displaystyle x{\small }\) сандары үшін \(\displaystyle ax^2<0\) болады. Так как все точки параболы лежат ниже оси \(\displaystyle \rm OX{ \small ,}\) то \(\displaystyle ax^2<0\) для всех ненулевых действительных чисел \(\displaystyle x{\small .}\)
\(\displaystyle x=1{\small }\) алмастырайық. \(\displaystyle a\cdot 1^2<0{\small }\) аламыз, яғни
\(\displaystyle a<0{\small .}\)
Егер \(\displaystyle y=ax^2\) параболасының тармақтары төмен бағытталған болса, онда \(\displaystyle x^2\) коэффициенті теріс болады, яғни
\(\displaystyle a<0{\small .}\)
