\(\displaystyle a\) және \(\displaystyle b\) оң сандар болғандықтан, біз \(\displaystyle a\) тең болатын қабырғасы бар шаршы құра аламыз (мысалы, сантиметр).

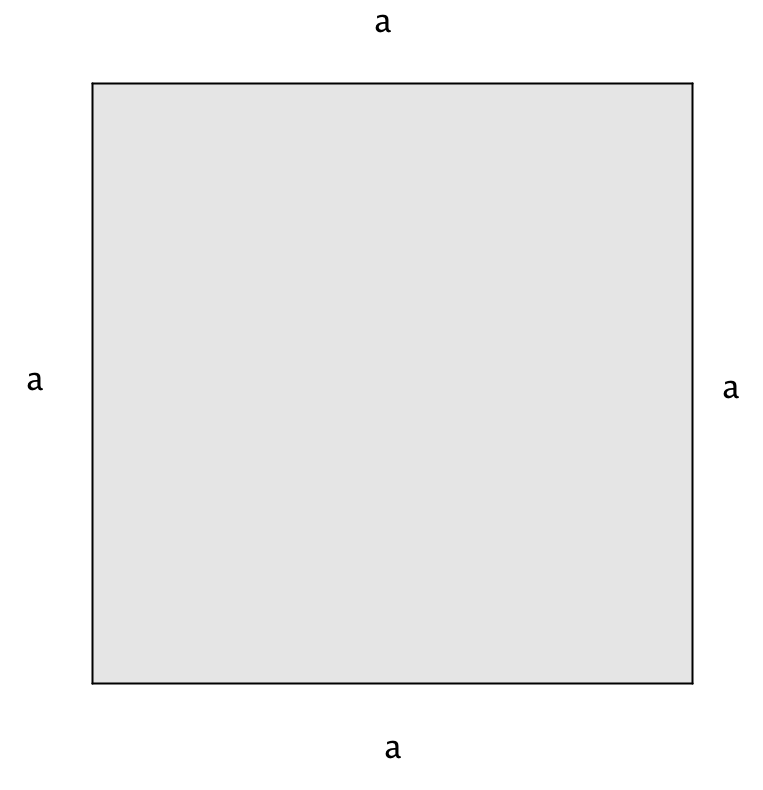
Берілген шаршының ауданы \(\displaystyle a^{\,2}\) тең (шаршы сантиметр). 

Шаршының әр жағын суретте көрсетілгендей ұзындығы \(\displaystyle a-b\) және \(\displaystyle b\) болатын екі бөлікке бөлейік:

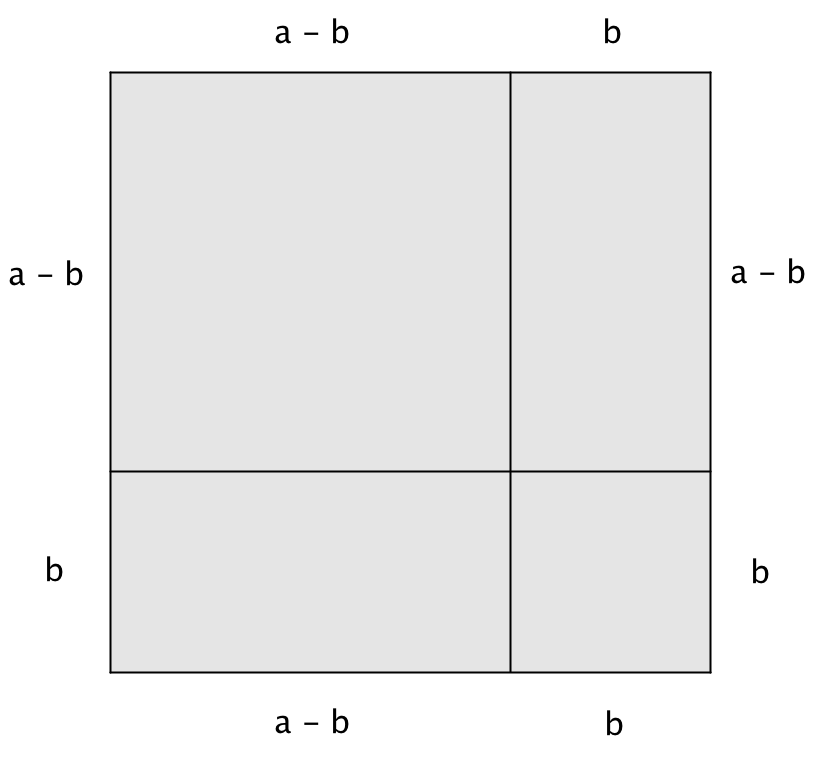
Қабырғасы \(\displaystyle a\) болатын шаршы келесілерден тұрады:

1) қабырғасы \(\displaystyle a - b\) болатын шаршы, 

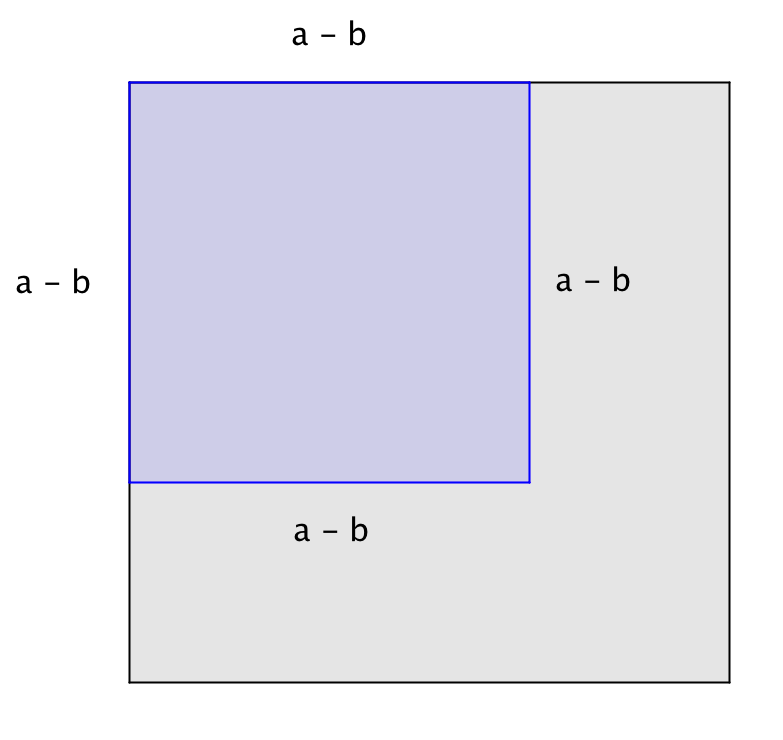
2) қабырғалары \(\displaystyle a\) және \(\displaystyle b\) болатын екі тіктөртбұрыш,

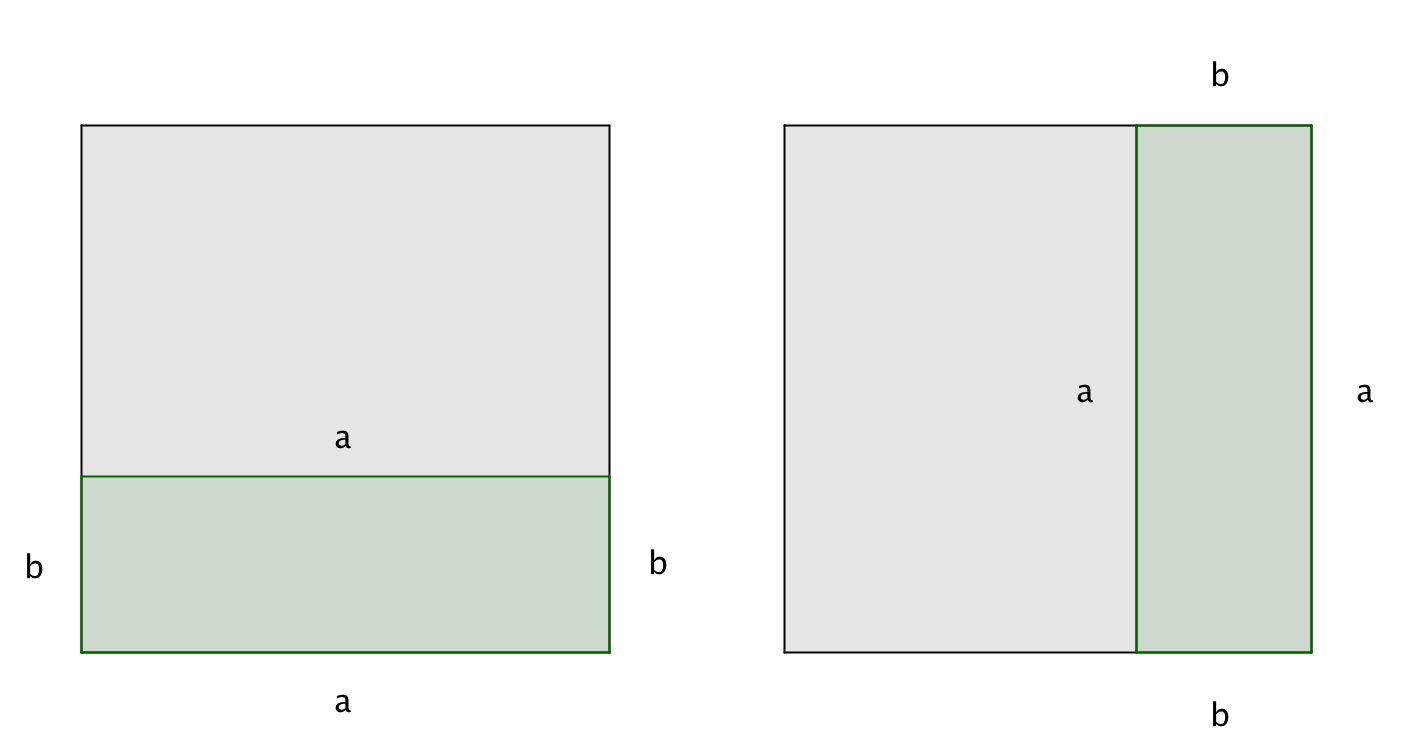
қабырғасы \(\displaystyle b\) болатын шаршыны қоспағанда:

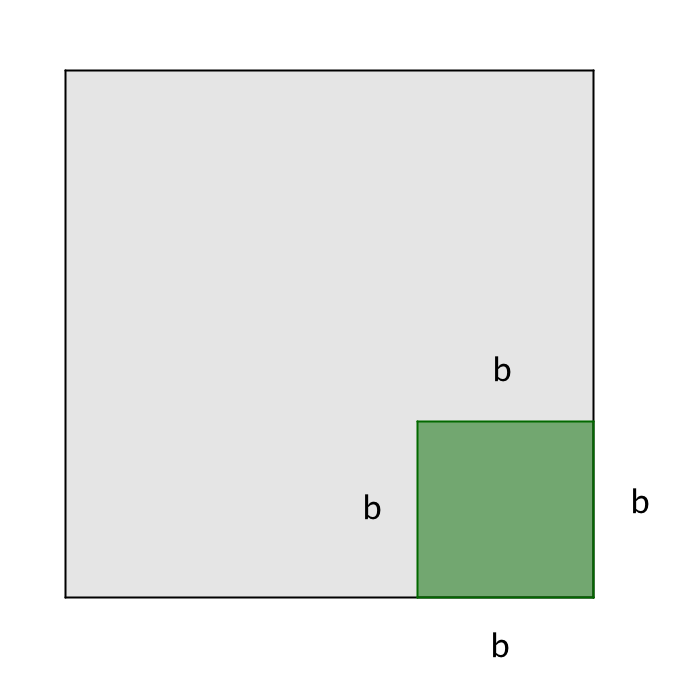
Сондықтан қабырғасы \(\displaystyle a\) болатын шаршының ауданы қабырғасы \(\displaystyle a-b\) болатын шаршының аудандарының, қабырғасы \(\displaystyle b\) болатын шаршының ауданын азайтқандағы қабырғалары \(\displaystyle a\) және \(\displaystyle b\) болатын екі тіктөртбұрыштың қосындысына тең. 

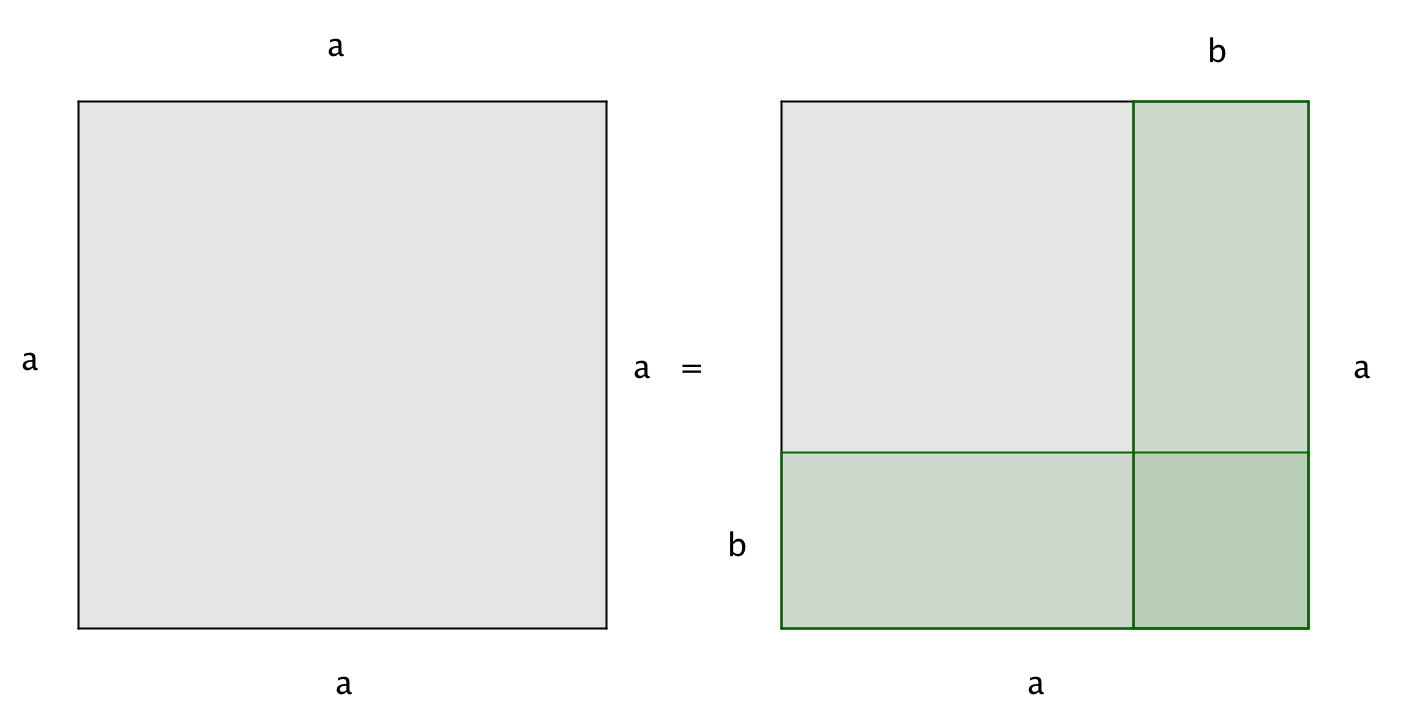
Үлкен шаршының ауданы оны құрайтын фигуралардың аудандарының қосындысына тең: 

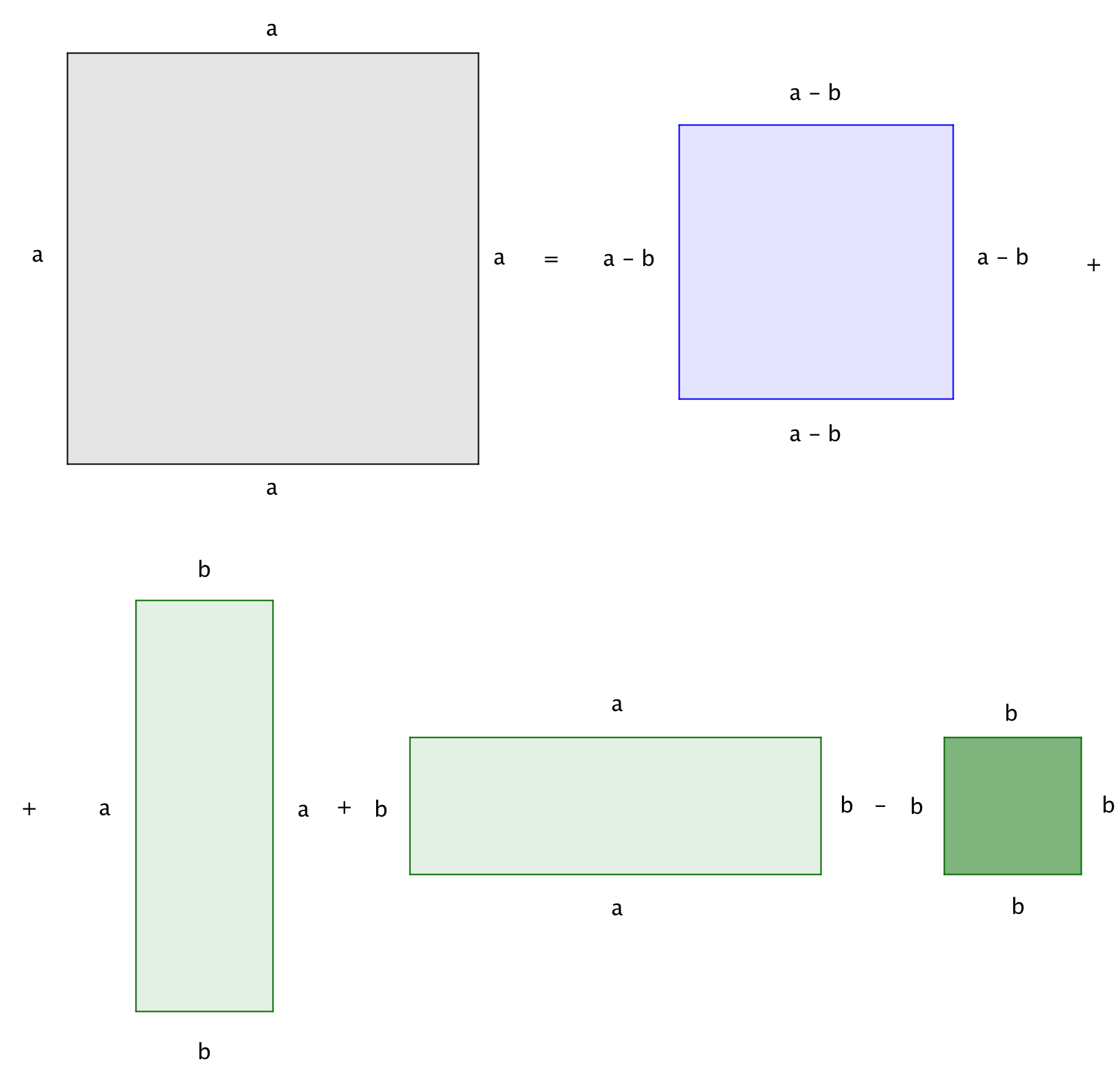
Фигуралардың әрқайсысының ауданын табайық.

Қабырғасы \(\displaystyle a\) болатын шаршының ауданы \(\displaystyle a^{\,2}\) тең: 

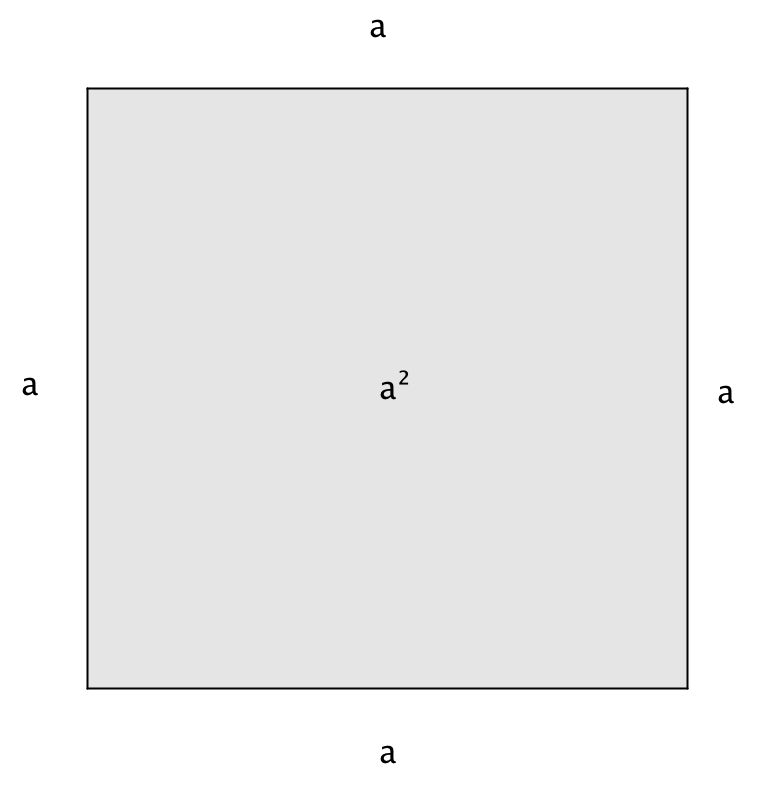\(\displaystyle =a^{\,2}\)

Қабырғасы \(\displaystyle a - b\) болатын шаршының ауданы \(\displaystyle (a-b\,)^2\) тең:  

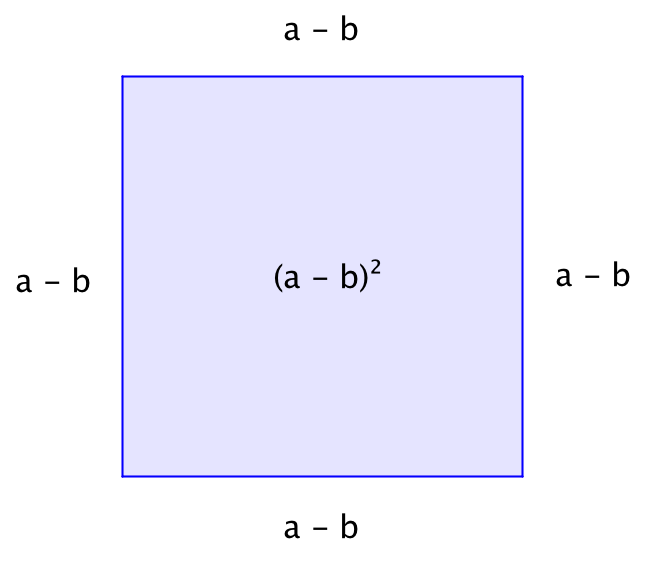\(\displaystyle =(a-b\,)^2\)

Қабырғалары \(\displaystyle a\) және \(\displaystyle b\) болатын тіктөртбұрыштардың әрқайсысының ауданы \(\displaystyle ab\) тең:

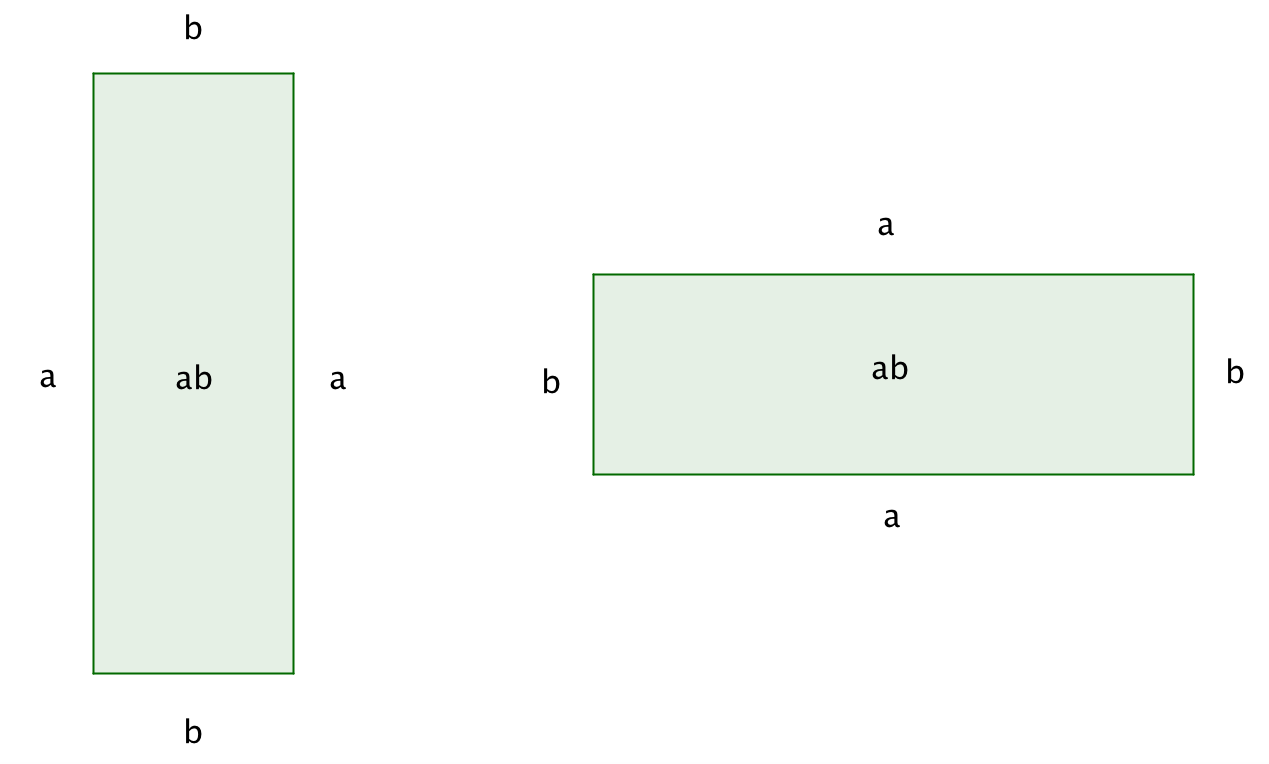\(\displaystyle =ab\)

Қабырғасы \(\displaystyle b\) болатын шаршының ауданы \(\displaystyle b^{\,2}\) тең:  

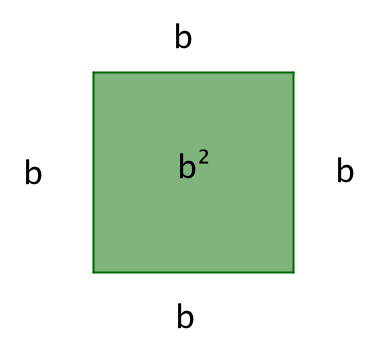\(\displaystyle =b^{\,2}\)

Қабырғасы \(\displaystyle a\) болатын шаршының ауданын екі тәсілмен табайық: анықтамасы бойынша және оны құрайтын фигуралардың аудандарының қосындысы ретінде. 

\(\displaystyle a^{\,2}=\)

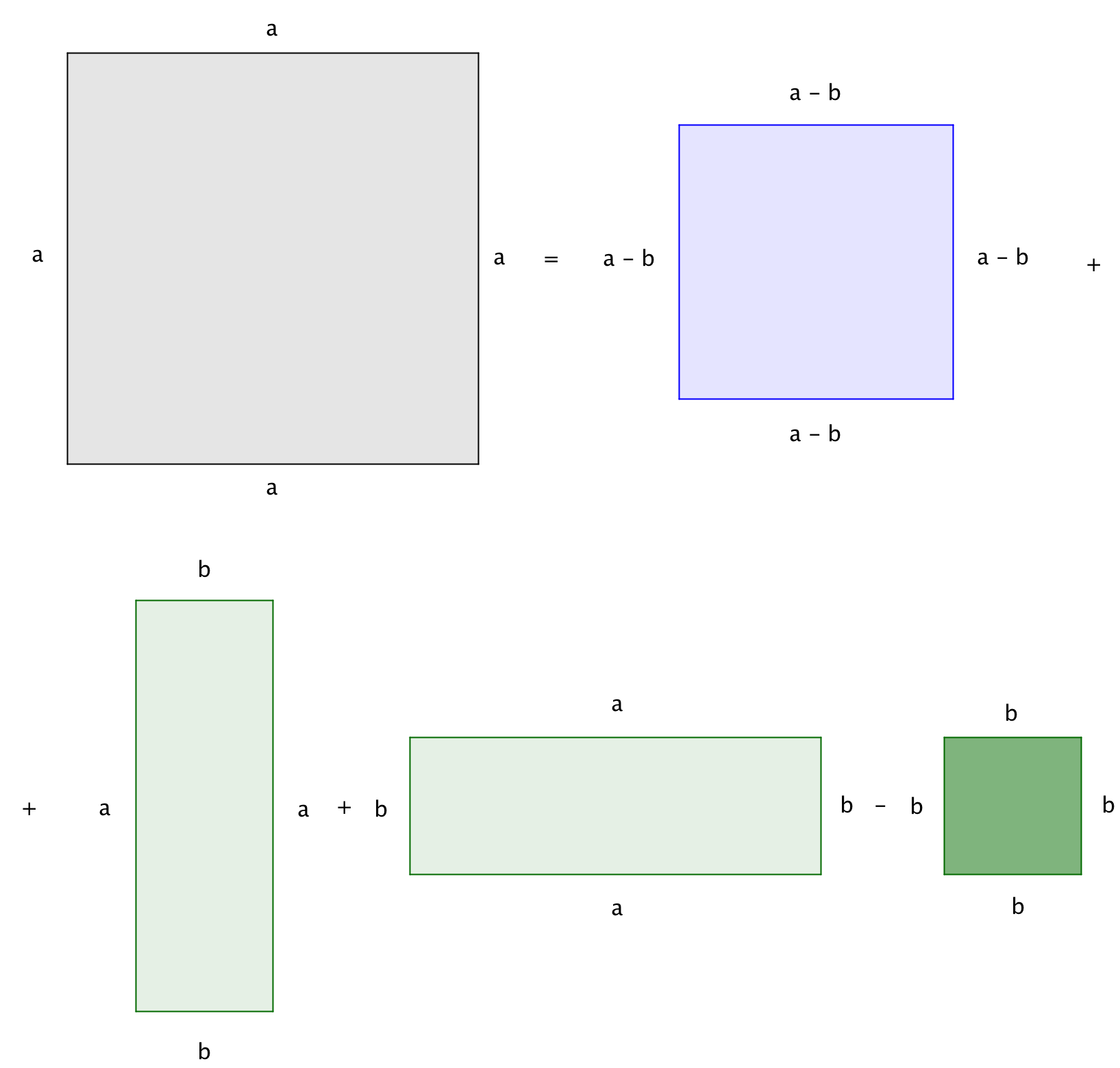\(\displaystyle =(a-b\,)^2+\underbrace{a\cdot b+a\cdot b}_{2ab}-b^{\,2}=(a-b\,)^2+2ab-b^{\,2}\)

Осылайша біз төмендегі формуланы алдық,

\(\displaystyle a^{\,2}=(a-b\,)^2+2ab-b^{\,2},\)

бұл жерден

\(\displaystyle (a-b\,)^2=a^{\,2}-2ab+b^{\,2}.\)