Тапсырма
\(\displaystyle y=\frac{5}{x}{\small }\) функциясының графигі берілген
\(\displaystyle a\) және \(\displaystyle b{ \small }\) жүгірткілерді жылжыту арқылы \(\displaystyle y=\frac{5}{x+1}+1{,}5{\small }\) функциясының графигін салыңыз.
\(\displaystyle a\) және \(\displaystyle b{\small }\) параметрлері
Алынған мәндерді жазыңыз:
\(\displaystyle \color{green}{A}=\)
.
Шешім
\(\displaystyle y=\frac{5}{x}\) гиперболасынан \(\displaystyle y=\frac{5}{x+1}+1{,}5{\small }\) функция графигін аламыз.
Ережені қолдану арқылы \(\displaystyle y=\frac{5}{x}\) гиперболасынан \(\displaystyle y=\frac{5}{x+1}{\small }\) функциясының графигін аламыз.
Правило
- Егер \(\displaystyle y=f(x) \) функциясының графигін \(\displaystyle \color{blue}{\rm A} \) бірлік оңға жылжытса \(\displaystyle y=f(x{\bf-}\color{blue}{\rm A}){\small } \) функциясының графигі шығады.
- Егер \(\displaystyle y=f(x) \) функциясының графигін \(\displaystyle \color{blue}{\rm A} \) бірлік солға жылжытса \(\displaystyle y=f(x{\bf+}\color{blue}{\rm A}){\small } \) функциясының графигі шығады.
\(\displaystyle 1\) бірлік оңға жылжуды аламыз:
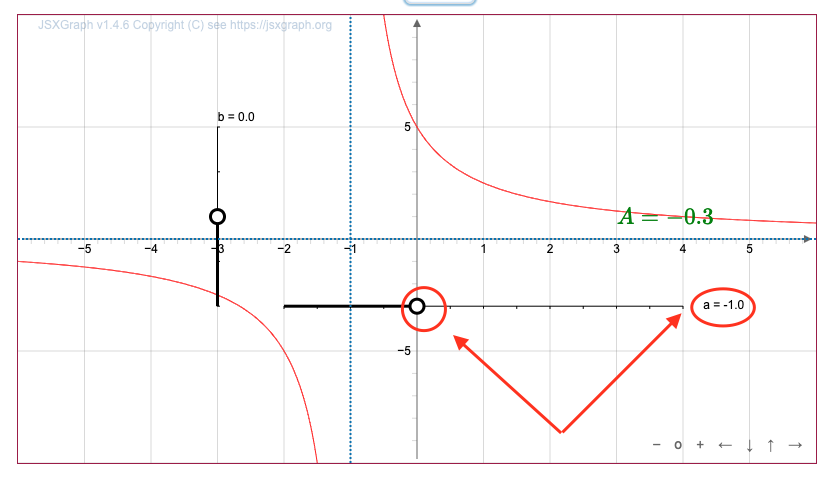
Ережені қолдану арқылы \(\displaystyle y=\frac{5}{x+1}\) функция графигін \(\displaystyle y=\frac{5}{x+1}+1{,}5{\small }\) аламыз.
Правило
- Егер \(\displaystyle y=f(x) \) функциясының графигін \(\displaystyle \color{blue}{\rm A} \) бірлік жоғары жылжытса \(\displaystyle y=f(x){\bf+}\color{blue}{\rm A}{\small } \) функциясының графигі шығады.
- Егер \(\displaystyle y=f(x) \) функциясының графигін \(\displaystyle \color{blue}{\rm A} \) бірлік төмен жылжытса \(\displaystyle y=f(x){\bf-}\color{blue}{\rm A}{\small } \) функциясының графигі шығады.
\(\displaystyle 1{,}5\) бірлік жоғары жылжуды аламыз:
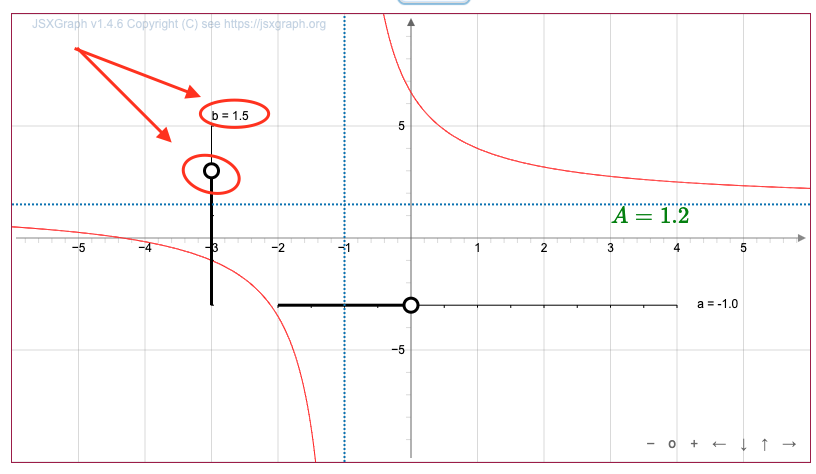
Сонда \(\displaystyle \color{green}{A}\) параметрі \(\displaystyle 1{,}2{\small }\) тең
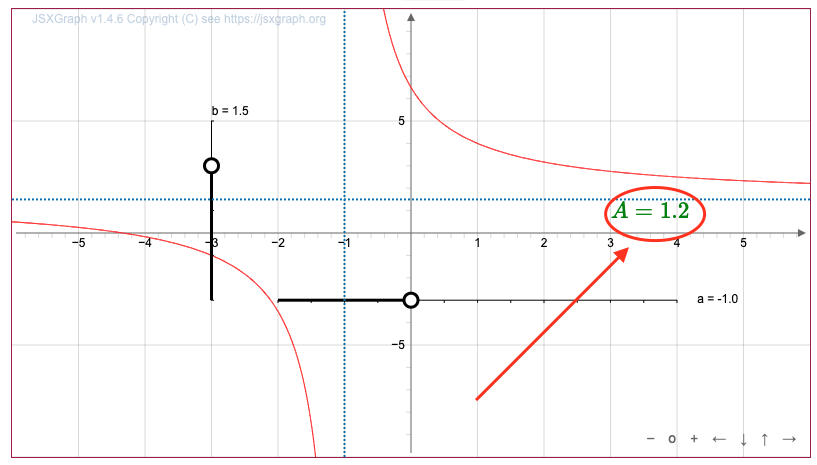
Жауабы:\(\displaystyle \color{green}{A}=1{,}2{\small .}\)
