Суретте \(\displaystyle A\) және \(\displaystyle B\) нүктелерінде қиылысатын \(\displaystyle f\left(x\right)=4x^2-25x+41\) және \(\displaystyle g\left(x\right)=ax^{2} +bx+c{ \small}\) функцияларының графиктері көрсетілген.
\(\displaystyle B\) нүктесінің абсциссасын табыңыз.
Есептің шарты бойынша, \(\displaystyle f\left(x\right)=4x^2-25x+41\) және \(\displaystyle g\left(x\right)=ax^2+bx+c\) функцияларының графиктері \(\displaystyle A\) және \(\displaystyle B\) нүктелерінде қиылысады.
Суретте \(\displaystyle A\) нүктесі көрінеді, бірақ \(\displaystyle B\) нүктесі жоқ.
\(\displaystyle f\left(x\right)=4x^2-25x+41{ \small}\) теңдеуімен параболалардың қайсысы берілгенін анықтайық.
Суреттің оң жағында көрсетілген параболаның шыңында ғана оң абсцисса бар екенін ескереміз.
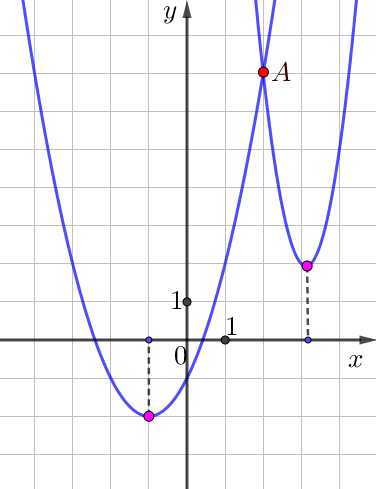
\(\displaystyle y=4x^2-25x+41{ \small }\) параболасы шыңының абсциссасын тауып, оның оң екенін тексерейік.
Парабола шыңының абсциссасы
\(\displaystyle y=\color{red}ax^2+\color{blue}bx+\color{green}c\) параболасының \(\displaystyle x_0\) абсциссасы келесі формуламен табылады:
\(\displaystyle x_0=\frac{-\color{blue}b\phantom{1}}{2\color{red}a}{\small.}\)
Онда біздің жағдайда
\(\displaystyle x_0=-\frac{ \color{blue}{-25}\phantom{1}}{2 \cdot \color{red} 4 }=\frac {25}{8}>0{ \small .}\)
Сонымен, \(\displaystyle y=4x^2-25x+41{ \small }\) теңдеуімен берілген парабола суреттің оң жағында көрсетілген.
Сонда коэффициенттері белгісіз теңдеумен берілген парабола суреттің сол жағында көрсетілген.
1. \(\displaystyle g\left(x\right)=ax^2+bx+c{ \small}\) параболасының теңдеуінен \(\displaystyle a{\small,}\) \(\displaystyle b\) және \(\displaystyle c{\small}\) коэффициенттерін табамыз.
Коэффициенттерді табу үшін \(\displaystyle a{\small,}\) \(\displaystyle b\) және \(\displaystyle c{\small}\) қатысты сызықтық теңдеулер жүйесін құрастырамыз және оны шешеміз.
\(\displaystyle A(\color{blue}{2};\color{blue}{7}){\small,}\)\(\displaystyle D(\color{green}{-1};\color{green}{-2})\) және \(\displaystyle C(\color{Purple}{-3};\color{Purple}{2})\) нүктелерінің \(\displaystyle g(x)=ax^2+bx+c{\small}\) функциясының графигінде жатқандығын пайдаланамыз.
Демек,
- \(\displaystyle x=\color{blue}{2}\) және \(\displaystyle y=\color{blue}{7}\) координаталарын \(\displaystyle y=ax^2+bx+c\) теңдеуіне қойғанда дұрыс теңдік аламыз;
- \(\displaystyle x=\color{green}{-1}\) және \(\displaystyle y=\color{green}{-2}\) координаталарын \(\displaystyle y=ax^2+bx+c\) теңдеуіне қойғанда дұрыс теңдік аламыз;
- \(\displaystyle x=\color{Purple}{-3}\) және \(\displaystyle y=\color{Purple}{2}\) координаталарын \(\displaystyle y=ax^2+bx+c\) теңдеуіне қойғанда дұрыс теңдік аламыз.
Осылайша, келесі теңдеулер жүйесін аламыз
\(\displaystyle \left\{\begin{aligned}\color{blue}{7}&\color{blue}{=a\cdot \color{blue}{2}^2+b\cdot \color{blue}{2}+c}{ \small ,}\\\color{green}{-2}&\color{green}{=a\cdot (\color{green}{-1})^2+b\cdot (\color{green}{-1})+c}{ \small ,}\\\color{Purple}{2}&\color{Purple}{=a \cdot (\color{Purple}{-3})^2+b\cdot (\color{Purple}{-3})+c} {\small .}\end{aligned}\right. \)
Немесе
\(\displaystyle \left\{\begin{aligned}4a+2b+c&=7{ \small ,}\\a-b+c&=-2{ \small ,}\\9a-3b+c&=2 {\small .}\end{aligned}\right. \)
Екінші теңдеуден \(\displaystyle c\)-ны \(\displaystyle a\) және \(\displaystyle b{\small}\) арқылы өрнектейміз:
\(\displaystyle c=-2-a+b{\small .}\)
Енді жүйенің бірінші және үшінші теңдеулеріндегі \(\displaystyle c\) орнына \(\displaystyle \color{Magenta}{-2-a+b}\) өрнегін қоямыз:
\(\displaystyle \left\{\begin{aligned}4a+2b+(\color{Magenta}{-2-a+b})&=7{ \small ,}\\9a-3b+(\color{Magenta}{-2-a+b})&=2 {\small .}\end{aligned}\right. \)
Немесе
\(\displaystyle \left\{\begin{aligned}{3a+3b=9}{ \small ,}\\{8a-2b=4} {\small .}\end{aligned}\right. \)
Алынған жүйені шешейік.
Үш теңдеуден тұратын бастапқы жүйенің шешімін табамыз.
Келесілерді пайдаланып,
\(\displaystyle c=-2-a+b\)
және
\(\displaystyle a=1\) және \(\displaystyle b=2{ \small .}\)
Төмендегіні аламыз:
\(\displaystyle c=-2-1+2=-1{ \small .}\)
Бастапқы жүйенің шешімі - сандар үштігі болып табылады.
\(\displaystyle a=1{ \small ,}\) \(\displaystyle b=2\) және \(\displaystyle c=-1{ \small .}\)
Демек, парабола теңдеуі келесідей болады:
\(\displaystyle g\left(x\right)=x^2+2x-1{ \small .}\)
2. \(\displaystyle B\) нүктесінің абсциссасын табамыз.
\(\displaystyle A\) және \(\displaystyle B\) нүктелері – \(\displaystyle f\left(x\right)=4x^2-25x+41\) және \(\displaystyle g\left(x\right)=x^2+2x-1{ \small}\) функция графиктерінің қиылысу нүктелері болып табылады.
Демек, бұл нүктелердің координаталары екі параболаның теңдеулерін қанағаттандырады:
\(\displaystyle \left\{\begin{aligned}y&=4x^2-25x+41{ \small ,}\\y&=x^2+2x-1{ \small .}\end{aligned}\right. \)
\(\displaystyle y=4x^2-25x+41\) және \(\displaystyle y=x^2+2x-1{ \small} \) болғандықтан, онда
\(\displaystyle 4x^2-25x+41 =x^2+2x-1 { \small .}\)
Барлығын сол жаққа жылжытайық:
\(\displaystyle 4x^2-25x+41-x^2-2x+1= 0 { \small ,} \)
\(\displaystyle 3x^2-27x+42 = 0 { \small .}\)
Алынған квадрат теңдеудің екі жағын да \(\displaystyle 3\) қысқартамыз:
\(\displaystyle x^2-9x+14 = 0 { \small .}\)
\(\displaystyle x^2-9x+14=0{ \small}\) квадрат теңдеуін шешейік.
Осылайша, \(\displaystyle f\left(x\right)=4x^2-25x+41\) және \(\displaystyle g\left(x\right)=x^2+2x-1\) функция графиктерінің қиылысу нүктелерінің абсциссалары келесіге тең
\(\displaystyle x_1=2\) және \(\displaystyle x_2=7{\small.}\)
\(\displaystyle x_1=2\) және \(\displaystyle x_2=7\) мәндері екі \(\displaystyle A \) және \(\displaystyle B\) қиылысу нүктелеріне сәйкес келеді.
Суреттен \(\displaystyle A \) нүктесінің абсциссасы \(\displaystyle 2\) тең екенін көреміз.
Демек, \(\displaystyle B\) нүктесіне \(\displaystyle x_2=7{\small}\) сәйкес келеді.
Осылайша, \(\displaystyle B\) нүктесінің абсциссасы \(\displaystyle 7\) тең.
Жауабы: \(\displaystyle 7{\small.}\)
