Деректер бағаналы диаграмма түрінде ұсынылған:
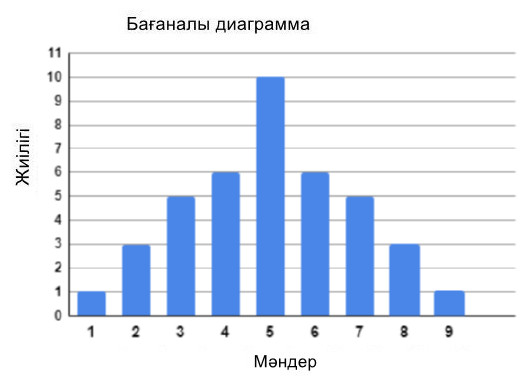
Бұл деректер жиынының орташа мәні:
\(\displaystyle \overline{x}=5\small.\)
Абсолютті ауытқулардың арифметикалық орташа мәнін табыңыз:
\(\displaystyle \frac{|x_1-\overline{x}|+|x_2-\overline{x}|+\dots+|x_n-\overline{x}|}{n}=\)
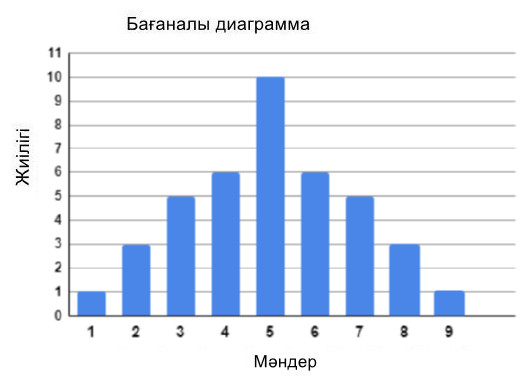
Деректер бағаналы диаграмма түрінде ұсынылған.
Деректер жиынының орташа мәні шарттан \(\displaystyle \overline{x}=5\) екені белгілі.
Диаграммаға сүйене отырып, жиілік кестесін жасайық. Сондай-ақ, кестеге орташа мәннен абсолютті ауытқулары бар қатарды қосайық.
Келесіні аламыз:
| \(\displaystyle (x)\) мәні | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 4\) | \(\displaystyle 5\) | \(\displaystyle 6\) | \(\displaystyle 7\) | \(\displaystyle 8\) | \(\displaystyle 9\) | |
| \(\displaystyle |x-\overline{x}|\) абсолютті ауытқу | \(\displaystyle 4\) | \(\displaystyle 3\) | \(\displaystyle 2\) | \(\displaystyle 1\) | \(\displaystyle 0\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 4\) | |
| Жиілік | \(\displaystyle 1\) | \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 6\) | \(\displaystyle 10\) | \(\displaystyle 6\) | \(\displaystyle 5\) | \(\displaystyle 3\) | \(\displaystyle 1\) | Сумма: \(\displaystyle 40\) |
Енді екінші және үшінші қатарды қолдана отырып, абсолютті ауытқулардың арифметикалық орташа мәнін табамыз:
\(\displaystyle \frac{4\cdot1+3\cdot3+2\cdot5+1\cdot6+0\cdot10+1\cdot6+2\cdot5+3\cdot3+4\cdot1}{24}=\frac{58}{40}=1{,}45\small.\)
Жауабы: \(\displaystyle 1{,}45\small.\)
