Данные представлены в виде столбчатой диаграммы:
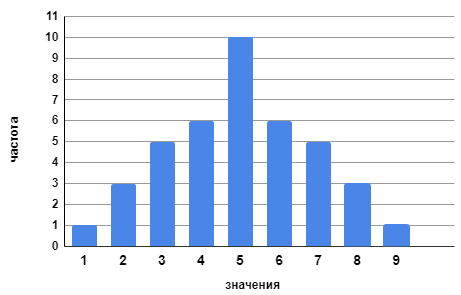
Известно среднее этого набора данных:
\(\displaystyle \overline{x}=5\small.\)
Найдите среднее арифметическое абсолютных отклонений от среднего:
\(\displaystyle \frac{|x_1-\overline{x}|+|x_2-\overline{x}|+\dots+|x_n-\overline{x}|}{n}=\)
Данные представлены в виде столбчатой диаграммы.
Среднее набора данных известно из условия: \(\displaystyle \overline{x}=5\small.\)
По диаграмме составим таблицу частот. Добавим также в таблицу строку с абсолютными отклонениями от среднего.

Получим:
| Значение \(\displaystyle (x)\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 4\) | \(\displaystyle 5\) | \(\displaystyle 6\) | \(\displaystyle 7\) | \(\displaystyle 8\) | \(\displaystyle 9\) | |
| Абсолютное отклонение \(\displaystyle |x-\overline{x}|\) | \(\displaystyle 4\) | \(\displaystyle 3\) | \(\displaystyle 2\) | \(\displaystyle 1\) | \(\displaystyle 0\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 4\) | |
| Частота | \(\displaystyle 1\) | \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 6\) | \(\displaystyle 10\) | \(\displaystyle 6\) | \(\displaystyle 5\) | \(\displaystyle 3\) | \(\displaystyle 1\) | Сумма: \(\displaystyle 40\) |
Теперь, используя вторую и третью строки, найдём среднее арифметическое абсолютных отклонений:
\(\displaystyle \frac{4\cdot1+3\cdot3+2\cdot5+1\cdot6+0\cdot10+1\cdot6+2\cdot5+3\cdot3+4\cdot1}{24}=\frac{58}{40}=1{,}45\small.\)
Ответ: \(\displaystyle 1{,}45\small.\)
