В остроугольном треугольнике \(\displaystyle ABC\) проведена высота \(\displaystyle BH {\small,}\) \(\displaystyle \angle BAC=37^{\circ} {\small.}\) Найдите угол \(\displaystyle ABH {\small.}\) Ответ дайте в градусах.
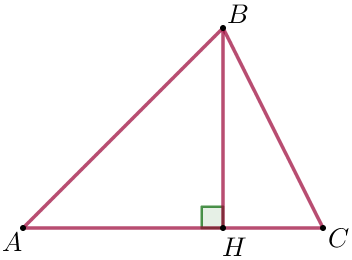
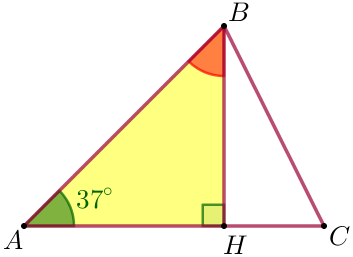 | Так как \(\displaystyle BH\) – высота треугольника \(\displaystyle ABC {\small,}\) то \(\displaystyle \triangle ABH\) – прямоугольный. Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ} {\small.}\) Тогда в прямоугольном треугольнике \(\displaystyle ABH {\small:}\) \(\displaystyle \angle ABH= 90^{\circ}- \angle BAH {\small,}\) \(\displaystyle \angle ABH= 90^{\circ}- 37^{\circ}= 53^{\circ} {\small.}\) |
Ответ: \(\displaystyle 53 {\small.}\)
