Какие из следующих утверждений верны?
\(\displaystyle 1)\) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
\(\displaystyle 2)\) Все диаметры окружности равны между собой.
\(\displaystyle 3)\) Один из углов треугольника всегда не превышает \(\displaystyle 60\) градусов.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Рассмотрим каждое утверждение:
\(\displaystyle 1)\) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
Для трапеции справедливо следующее утверждение:
Диагонали трапеции пересекаются и делятся точкой пересечения на отрезки, пропорциональные основаниям трапеции. \(\displaystyle \frac{AO}{OC}= \frac{DO}{OB}= \frac{AD}{BC}\) | 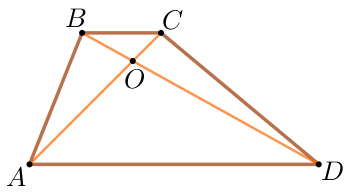 |
Утверждение \(\displaystyle 1)\) будет верно, если в нём слово "трапеция" заменить на слово "параллелограмм".
Свойство параллелограмма
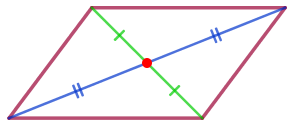 | Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам. |
\(\displaystyle 2)\) Все диаметры окружности равны между собой.
Окружность – это множество всех точек плоскости, находящихся на одинаковом расстоянии от данной точки. Радиус окружности – отрезок, соединяющий любую её точку с центром. | 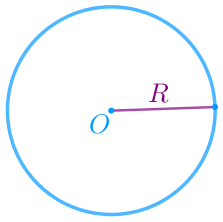 |
Все радиусы окружности равны.
Диаметр – отрезок, соединяющий две точки окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам. | 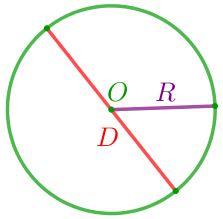 |
Все диаметры окружности равны.
\(\displaystyle 3)\) Один из углов треугольника всегда не превышает \(\displaystyle 60\) градусов.
Сумма углов треугольника равна \(\displaystyle 180^{\circ}{\small.}\\ \) \(\displaystyle \color{red}{\alpha}+\color{green}{\beta}+\color{blue}{\gamma}=180^{\circ}\) |
Значит, меньший угол в треугольнике \(\displaystyle \leq 60^{\circ} {\small.}\) Следовательно, в любом треугольнике есть угол, не превышающий \(\displaystyle 60\) градусов.
Ответ: \(\displaystyle 23 {\small.}\)
