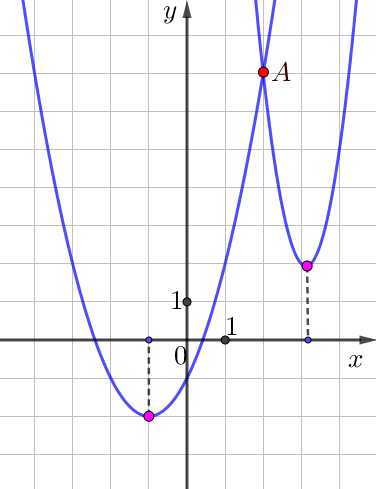
На рисунке изображены графики функций \(\displaystyle f\left(x\right)=4x^2-25x+41\) и \(\displaystyle g\left(x\right)=ax^{2} +bx+c{ \small ,}\) которые пересекаются в точках \(\displaystyle A\) и \(\displaystyle B{ \small .}\)
Найдите абсциссу точки \(\displaystyle B{ \small .}\)
По условию задачи графики функций \(\displaystyle f\left(x\right)=4x^2-25x+41\) и \(\displaystyle g\left(x\right)=ax^2+bx+c\) пересекаются в точках \(\displaystyle A\) и \(\displaystyle B{ \small .}\)
Точку \(\displaystyle A\) видно на рисунке, а точку \(\displaystyle B\) – нет.
Определим, какая из парабол задана уравнением \(\displaystyle f\left(x\right)=4x^2-25x+41{ \small .}\)
Заметим, что положительную абсциссу имеет только вершина параболы, которая изображена на рисунке правее.
Найдём абсциссу вершины параболы \(\displaystyle y=4x^2-25x+41{ \small }\) и проверим, положительна ли она.
Абсцисса вершины параболы
Абсцисса \(\displaystyle x_0\) вершины параболы \(\displaystyle y=\color{red}ax^2+\color{blue}bx+\color{green}c\) находится по формуле:
\(\displaystyle x_0=\frac{-\color{blue}b\phantom{1}}{2\color{red}a}{\small.}\)
Тогда в нашем случае
\(\displaystyle x_0=-\frac{ \color{blue}{-25}\phantom{1}}{2 \cdot \color{red} 4 }=\frac {25}{8}>0{ \small .}\)
Итак, парабола, заданная уравнением \(\displaystyle y=4x^2-25x+41{ \small }\) изображена на рисунке правее.
Тогда парабола, заданная уравнением с неизвестными коэффициентами, изображена на рисунке левее.
1. Найдем коэффициенты \(\displaystyle a{\small,}\) \(\displaystyle b\) и \(\displaystyle c{\small}\) из уравнения параболы \(\displaystyle g\left(x\right)=ax^2+bx+c{ \small .}\)
Чтобы найти коэффициенты, составим систему линейных уравнений относительно \(\displaystyle a{\small,}\) \(\displaystyle b\) и \(\displaystyle c{\small}\)
и решим её.
Воспользуемся тем, что точки \(\displaystyle A(\color{blue}{2};\color{blue}{7}){\small,}\)\(\displaystyle D(\color{green}{-1};\color{green}{-2})\) и \(\displaystyle C(\color{Purple}{-3};\color{Purple}{2})\) лежат на графике функции \(\displaystyle g(x)=ax^2+bx+c{\small.}\)
Значит,
- при подстановке координат \(\displaystyle x=\color{blue}{2}\) и \(\displaystyle y=\color{blue}{7}\) в уравнение \(\displaystyle y=ax^2+bx+c\) получим верное равенство;
- при подстановке координат \(\displaystyle x=\color{green}{-1}\) и \(\displaystyle y=\color{green}{-2}\) в уравнение \(\displaystyle y=ax^2+bx+c\) получим верное равенство;
- при подстановке координат \(\displaystyle x=\color{Purple}{-3}\) и \(\displaystyle y=\color{Purple}{2}\) в уравнение \(\displaystyle y=ax^2+bx+c\) получим верное равенство.
Таким образом, получаем систему уравнений
\(\displaystyle \left\{\begin{aligned}\color{blue}{7}&\color{blue}{=a\cdot \color{blue}{2}^2+b\cdot \color{blue}{2}+c}{ \small ,}\\\color{green}{-2}&\color{green}{=a\cdot (\color{green}{-1})^2+b\cdot (\color{green}{-1})+c}{ \small ,}\\\color{Purple}{2}&\color{Purple}{=a \cdot (\color{Purple}{-3})^2+b\cdot (\color{Purple}{-3})+c} {\small .}\end{aligned}\right. \)
Или
\(\displaystyle \left\{\begin{aligned}4a+2b+c&=7{ \small ,}\\a-b+c&=-2{ \small ,}\\9a-3b+c&=2 {\small .}\end{aligned}\right. \)
Выразим из второго уравнения \(\displaystyle c\) через \(\displaystyle a\) и \(\displaystyle b{\small : }\)
\(\displaystyle c=-2-a+b{\small .}\)
Теперь подставим выражение \(\displaystyle \color{Magenta}{-2-a+b}\) вместо \(\displaystyle c\) в первое и третье уравнения системы:
\(\displaystyle \left\{\begin{aligned}4a+2b+(\color{Magenta}{-2-a+b})&=7{ \small ,}\\9a-3b+(\color{Magenta}{-2-a+b})&=2 {\small .}\end{aligned}\right. \)
Или
\(\displaystyle \left\{\begin{aligned}{3a+3b=9}{ \small ,}\\{8a-2b=4} {\small .}\end{aligned}\right. \)
Решим полученную систему.
Найдём решение исходной системы из трёх уравнений.
Воспользуемся тем, что
\(\displaystyle c=-2-a+b\)
и
\(\displaystyle a=1\) и \(\displaystyle b=2{ \small .}\)
Получим:
\(\displaystyle c=-2-1+2=-1{ \small .}\)
Решением исходной системы является тройка чисел
\(\displaystyle a=1{ \small ,}\) \(\displaystyle b=2\) и \(\displaystyle c=-1{ \small .}\)
Значит, уравнение параболы имеет вид:
\(\displaystyle g\left(x\right)=x^2+2x-1{ \small .}\)
2. Найдем абсциссу точки \(\displaystyle B{ \small .}\)
Точки \(\displaystyle A\) и \(\displaystyle B\) – это точки пересечения графиков функций \(\displaystyle f\left(x\right)=4x^2-25x+41\) и \(\displaystyle g\left(x\right)=x^2+2x-1{ \small .}\)
Значит, координаты этих точек удовлетворяют уравнениям обеих парабол:
\(\displaystyle \left\{\begin{aligned}y&=4x^2-25x+41{ \small ,}\\y&=x^2+2x-1{ \small .}\end{aligned}\right. \)
Так как \(\displaystyle y=4x^2-25x+41\) и \(\displaystyle y=x^2+2x-1{ \small ,} \) то
\(\displaystyle 4x^2-25x+41 =x^2+2x-1 { \small .}\)
Перенесем все в левую часть:
\(\displaystyle 4x^2-25x+41-x^2-2x+1= 0 { \small ,} \)
\(\displaystyle 3x^2-27x+42 = 0 { \small .}\)
Сократим обе части полученного квадратного уравнения на \(\displaystyle 3 { \small :}\)
\(\displaystyle x^2-9x+14 = 0 { \small .}\)
Решим квадратное уравнение \(\displaystyle x^2-9x+14=0{ \small .}\)
Таким образом, абсциссы точек пересечения графиков функций \(\displaystyle f\left(x\right)=4x^2-25x+41\) и \(\displaystyle g\left(x\right)=x^2+2x-1\) равны
\(\displaystyle x_1=2\) и \(\displaystyle x_2=7{\small.}\)
Значения \(\displaystyle x_1=2\) и \(\displaystyle x_2=7\) соответствуют двум точкам пересечения \(\displaystyle A \) и \(\displaystyle B{\small .} \)
По рисунку видим, что абсцисса точки \(\displaystyle A \) равна \(\displaystyle 2{\small .}\)
Значит, точке \(\displaystyle B\) соответствует \(\displaystyle x_2=7{\small.}\)
Таким образом, абсцисса точки \(\displaystyle B\) равна \(\displaystyle 7{\small.}\)
Ответ: \(\displaystyle 7{\small.}\)
