Сәуледегі кез-келген нүктенің координатасы\(\displaystyle O(0)\)нүктесінен берілген нүктеге дейінгі қашықтыққа, яғни осы қашықтықта орналасқан бірлік кесінділердің ұзындығының қосындысына тең.

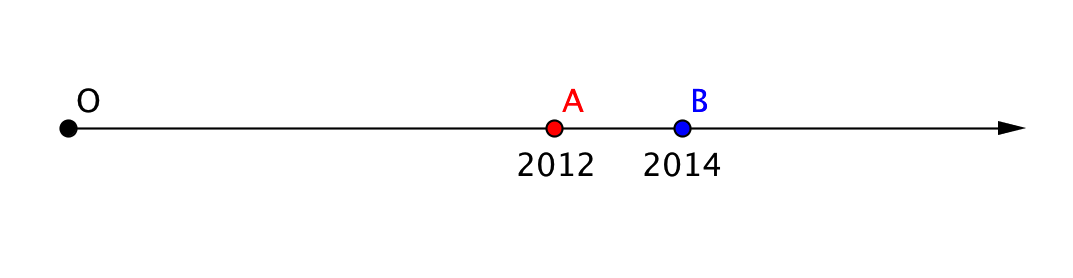
Координаттық сәуледе \(\displaystyle A(2012)\)және\(\displaystyle B(2014)\)нүктелерін бейнелейік. Бұл нүктелердің координаталары бірлік кесіндісінің соңындағы координатамен салыстырғанда үлкен болғандықтан (\(\displaystyle 1\)-ге тең ), онда бірлік кесіндінің өзі суретте көрсетпейміз. Сонымен қатар, бізді тек \(\displaystyle A\)және \(\displaystyle B\)нүктелерінің өзара орналасуы қызықтырады , сондықтан масштабты қолданбаймыз:

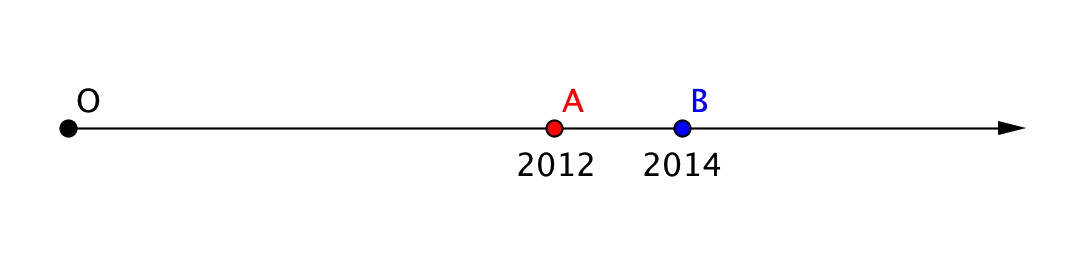
Суреттен көрініп тұрғандай, \(\displaystyle O\)нүктесінен \(\displaystyle A\)нүктесіне дейінгі қашықтық \(\displaystyle 2012\)бірлік кесінді ұзындығының қосындысына тең. Осылайша, \(\displaystyle A\)нүктесінің координатасы \(\displaystyle 2012\)тең және \(\displaystyle A(2012)\)деп белгіленеді.

 \(\displaystyle O\)нүктесінен \(\displaystyle B\)нүктесіне дейінгі қашықтық \(\displaystyle 2012\)бірлік кесінді ұзындығының қосындысына тең. Сондықтан \(\displaystyle B\)нүктесінің координатасы \(\displaystyle 2012\)тең және \(\displaystyle B(2014)\)деп белгіленеді.

Яғни ,\(\displaystyle A(2012)\)және B(2014) нүктелерінің арасындағы қашықтық AB кесіндісінің ұзындығына немесе оның оң және сол жақ ұштарының координаталарының айырмасына тең, яғни тиісінше\(\displaystyle A(2012)\)және\(\displaystyle B(2014)\)нүктелерінің координаталарына тең:

\(\displaystyle AB=OB-OA=2014-2012=2\).

Жауабы: \(\displaystyle 2\).