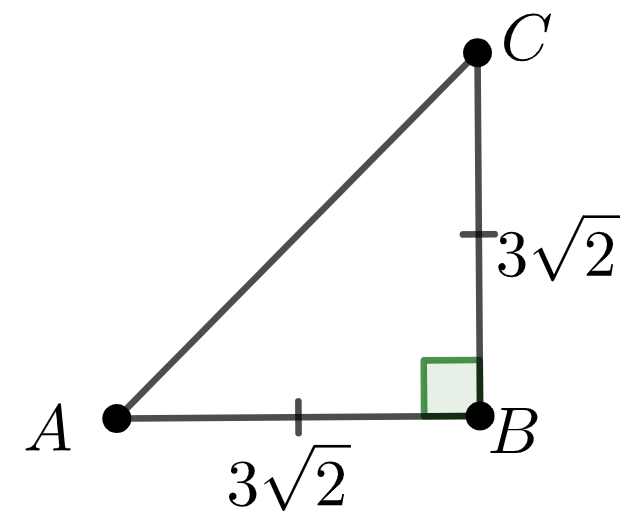
Дұрыс төртбұрышты пирамидада табанының қабырғасы \(\displaystyle 3\sqrt{2}{\small ,}\) және көлемі \(\displaystyle 24{\small }\) тең. Бүйір қабырғасын табыңыз..
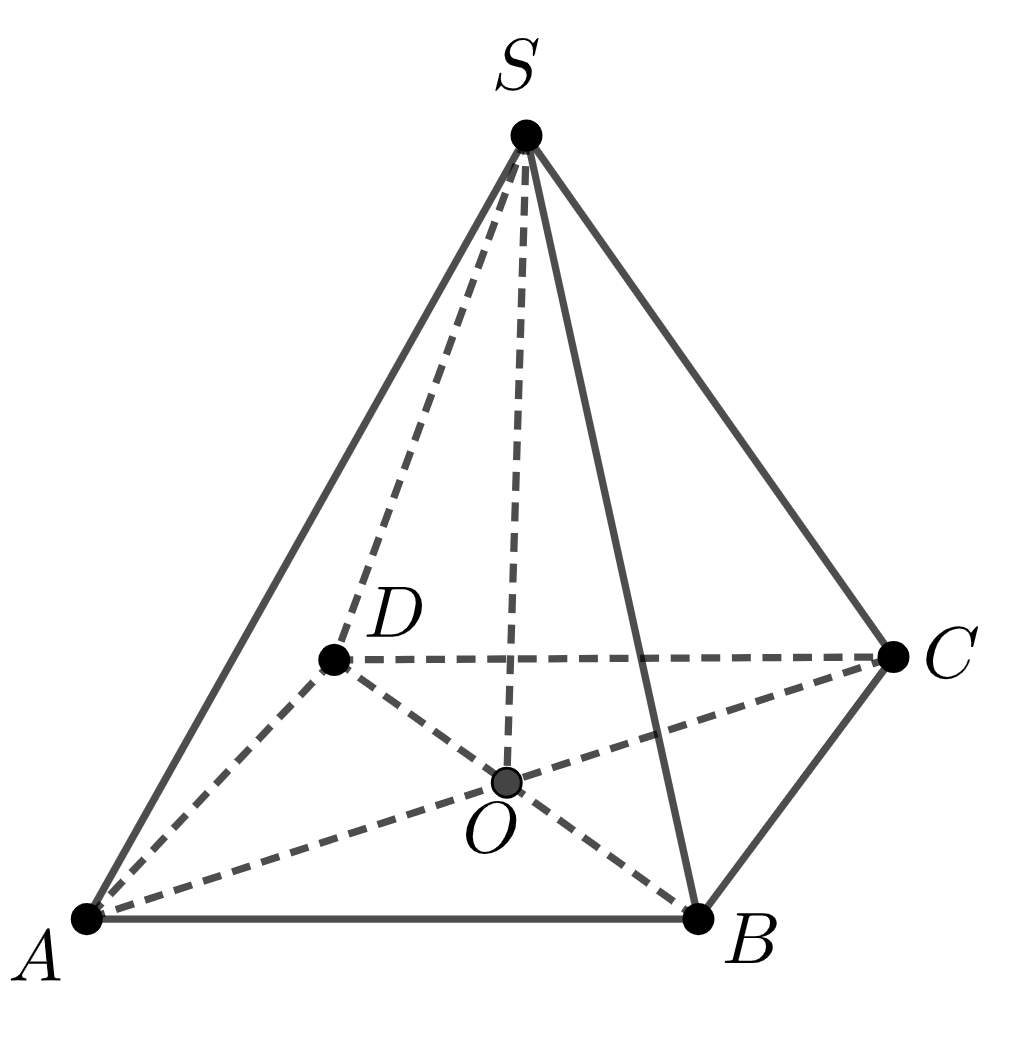
Дұрыс пирамида
Пирамида, егер оның табаны - дұрыс көпбұрыш, ал пирамиданың төбесін табанның центрімен байланыстыратын кесінді оның биіктігі болса, дұрыс деп аталады.
\(\displaystyle ABCD\)– осы пирамиданың табаны, \(\displaystyle SO\) биіктігі, \(\displaystyle S\) төбесі болсын.
Түзу жазықтықтағы кез келген түзуге перпендикуляр болса, ол жазықтыққа перпендикуляр деп аталады.Түзу мен жазықтықтың перпендикулярлығы
\(\displaystyle SO\) – \(\displaystyle SABCD\) пирамидасының биіктігі, яғни \(\displaystyle SO\) - \(\displaystyle OC \) жатқан табан жазықтығына перпендикуляр
Демек, \(\displaystyle SO\perp АC{\small .}\)
\(\displaystyle SАC{\small }\) үшбұрышын қарастырайық
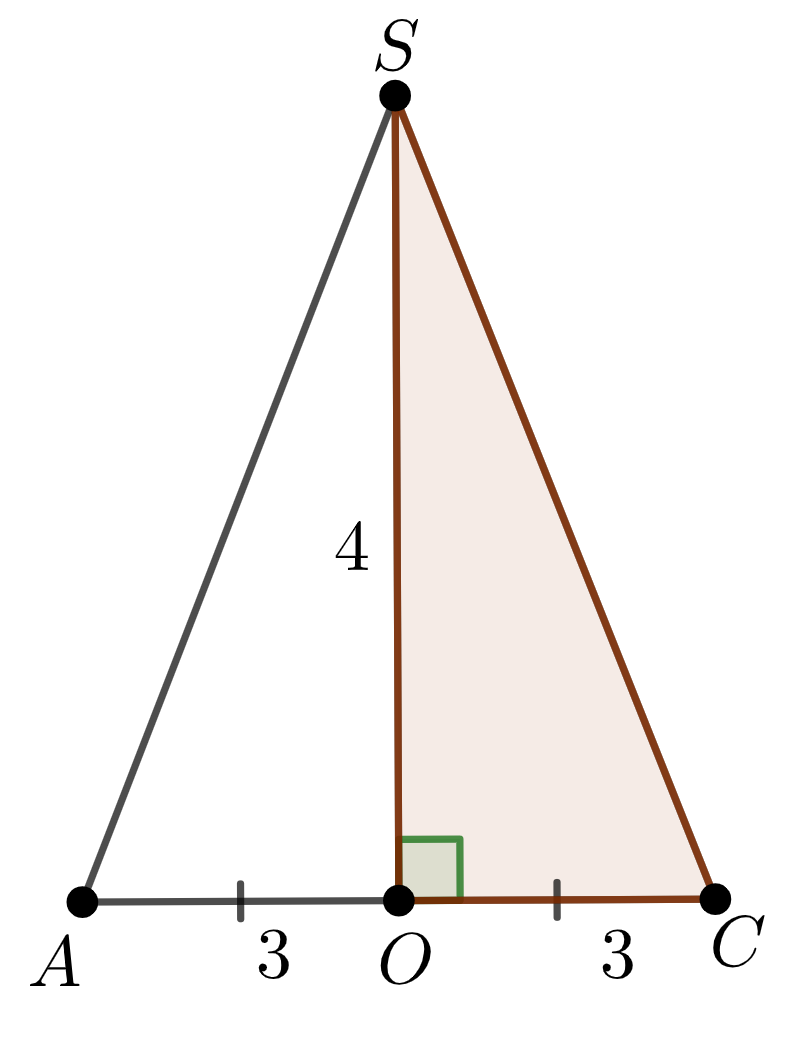
\(\displaystyle SOC \) үшбұрышы үшін Пифагор теоремасын пайдаланып \(\displaystyle SC\) табайық
\(\displaystyle SO^2+OC^2=SC^2{\small,}\)
\(\displaystyle 4^2+3^2=SC^2{\small ,}\)
\(\displaystyle SC^2=25{\small .}\)
Кесіндінің ұзындығы оң болғандықтан, , онда
\(\displaystyle SC=5{\small .}\)
Жауабы: \(\displaystyle 5{\small .}\)