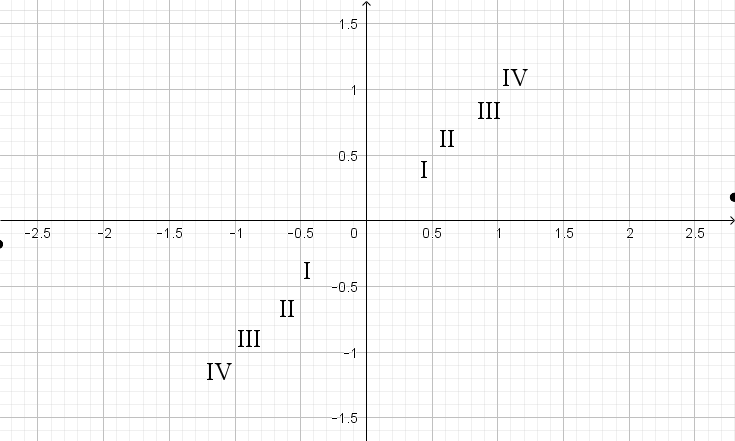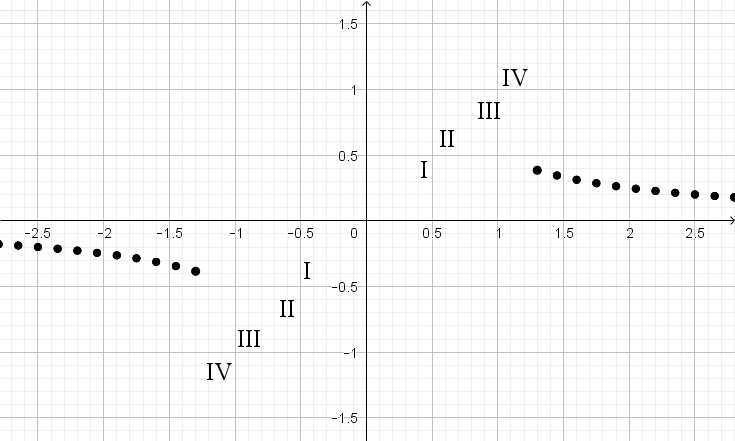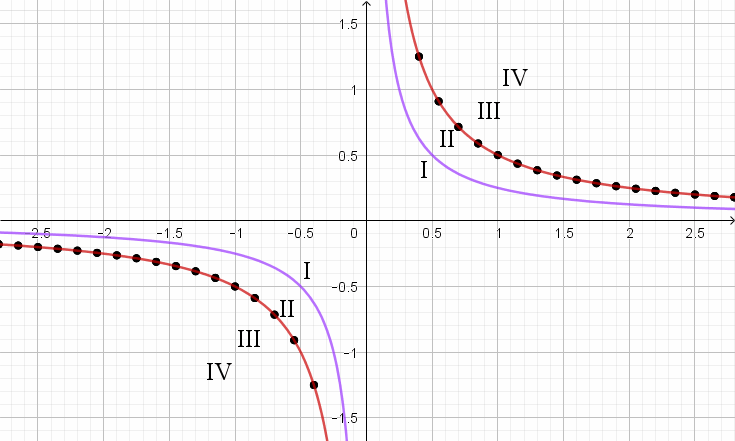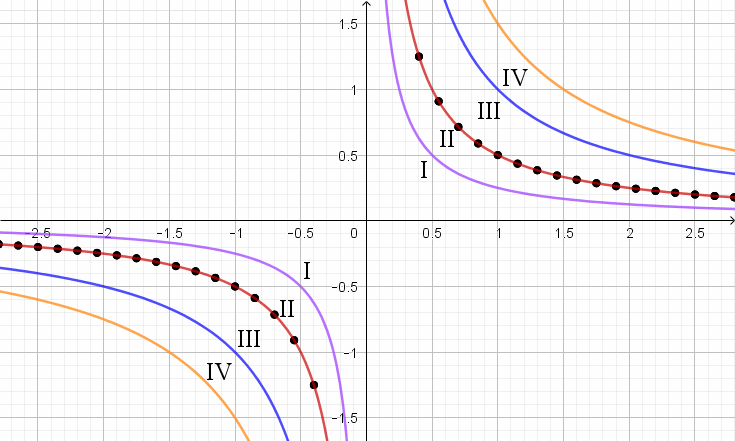1) График  \(\displaystyle \rm I {\small.}\)

Графикте \(\displaystyle \rm I\) гиперболасы \(\displaystyle (0{,}5;\, 0{,}5){\small }\) координаттары бар нүкте арқылы өтетінін көруге болады:

Бұл нүкте \(\displaystyle y=\frac{1}{2x}{\small }\) функциясының графигінде жатқанын тексеріңіз, оның координаттарын теңдеуге ауыстырыңыз:

\(\displaystyle 0{,}5=\frac{1}{2 \cdot 0{,}5}{\small ,}\)

\(\displaystyle 0{,}5=\frac{1}{1}{\small ,}\)

\(\displaystyle 0{,}5=1{\small .}\)

Дұрыс емес теңдік алынды.

Демек, бұл нүкте \(\displaystyle y=\frac{1}{2x}{\small }\) функция графигінде жатпайды.

Осылайша, \(\displaystyle \rm I\) гиперболасы \(\displaystyle y=\frac{1}{2x}{\small }\) функцияның графигі емес.

2) График \(\displaystyle \rm II {\small.}\)

Графикте  \(\displaystyle \rm II\) гиперболасы \(\displaystyle (0{,}5;\, 1){\small }\) координаттары бар нүкте арқылы өтетінін көруге болады:

Бұл нүкте \(\displaystyle y=\frac{1}{2x}{\small ,}\) функциясының графигінде жатқанын тексеріңіз, оның координаттарын теңдеуге ауыстырыңыз:

\(\displaystyle 1=\frac{1}{2 \cdot 0{,}5}{\small ,}\)

\(\displaystyle 1=\frac{1}{1}{\small ,}\)

\(\displaystyle 1 = 1{\small .}\)

Дұрыс теңдік алынды.

Демек, бұл нүкте \(\displaystyle y=\frac{1}{2x}{\small }\) функциясының графигінде жатыр.

Осылайша \(\displaystyle \rm II\) гипербола  \(\displaystyle y=\frac{1}{2x}{\small }\) функцияның графигі болып табылады

3) График \(\displaystyle \rm III {\small.}\)

Графикте \(\displaystyle \rm III\) гиперболасы \(\displaystyle (1;1){\small }\) координаттары бар нүкте арқылы өтетінін көруге болады:

Бұл нүкте \(\displaystyle y=\frac{1}{2x}{\small ,}\) функциясының графигінде жатқанын тексеріңіз, оның координаттарын теңдеуге ауыстырыңыз:

\(\displaystyle 1=\frac{1}{2 \cdot 1}{\small ,}\)

\(\displaystyle 1=\frac{1}{2}{\small ,}\)

\(\displaystyle 1 =0{,}5{\small .}\)

Дұрыс емес теңдік алынды.

Демек, бұл нүкте \(\displaystyle y=\frac{1}{2x}{\small }\) функция графигінде жатпайды.

Осылайша \(\displaystyle \rm III\) гипербола  \(\displaystyle y=\frac{1}{2x}{\small }\) функцияның графигі емес.

4) График \(\displaystyle \rm IV {\small.}\)

Графикте  \(\displaystyle \rm IV\) гиперболасы \(\displaystyle (1{,}5;\, 1){\small }\) координаттары бар нүкте арқылы өтетінін көруге болады:

Бұл нүкте \(\displaystyle y=\frac{1}{2x}{\small ,}\) функциясының графигінде жатқанын тексеріңіз, оның координаттарын теңдеуге ауыстырыңыз:

\(\displaystyle 1=\frac{1}{2 \cdot 1{,}5}{\small ,}\)

\(\displaystyle 1=\frac{1}{3}{\small ,}\)

Дұрыс емес теңдік алынды.

Демек, бұл нүкте \(\displaystyle y=\frac{1}{2x}{\small }\) функция графигінде жатпайды.

Осылайша \(\displaystyle \rm IV\) гипербола  \(\displaystyle y=\frac{1}{2x}{\small }\) функцияның графигі емес.

Демек \(\displaystyle \rm II\) гиперболасы \(\displaystyle y=\frac{1}{2x}{\small }\) функциясының графигі болып табылады   .

Жауап: \(\displaystyle \rm II {\small .}\)