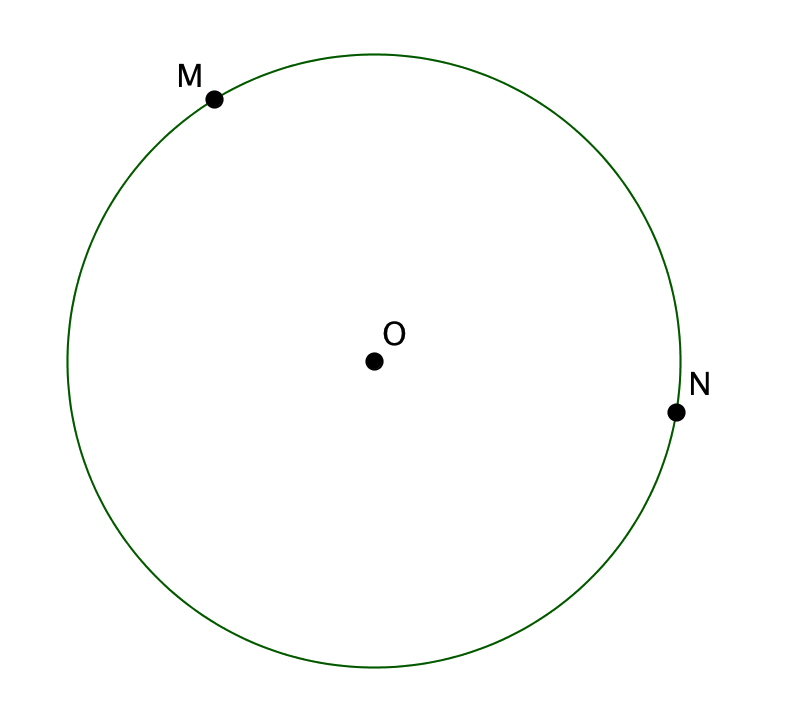
Сколько дуг окружности показано на рисунке?
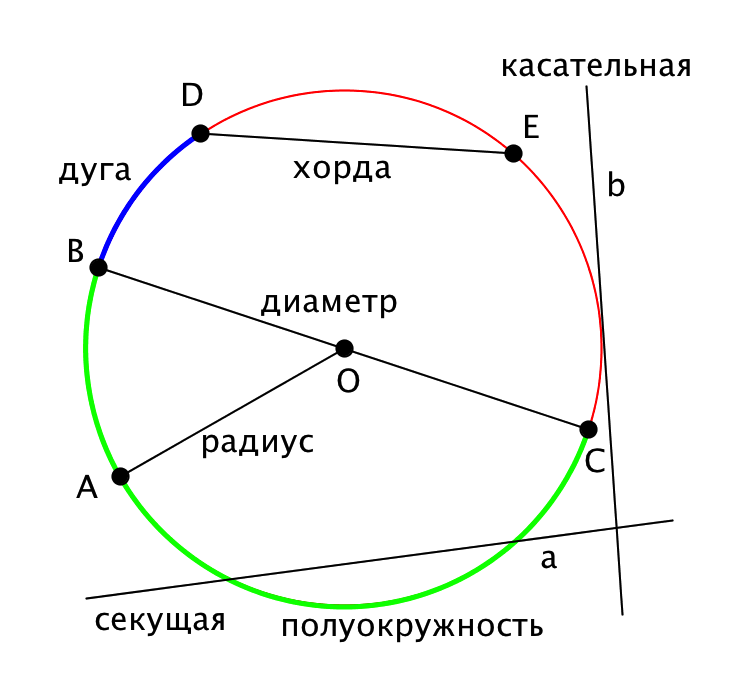
Отрезок, соединяющий центр окружности с любой из ее точек, называется ее радиусом.
Прямая, проходящая через любые две очки окружности, называется секущей.
Хорда - отрезок секущей, соединяющий две точки окружности (хорда - это отрезок, соединяющий две точки окружности).
Диаметр - хорда, проходящая через центр окружности.
Дуга - часть окружности.
Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром.
Касательная - прямая, имеющая с окружностью только одну общую точку.
Посчитаем количество частей окружности, ограниченных точками \(\displaystyle M\), \(\displaystyle N\). Ими являются две дуги \(\displaystyle MN\) (поскольку от точки \(\displaystyle M\) до точки \(\displaystyle N\) можно идти вдоль окружности как по часовой, так и против часовой стрелки). Таким образом, количество дуг окружности, показанной на рисунке, равно \(\displaystyle 2\).
Ответ: \(\displaystyle 2\) дуги окружности.
