Задание
Построение графика квадратичной функция \(\displaystyle y=2x^2\) на отрезке \(\displaystyle [-1; 1] \small .\)
Решение
Заполним таблицу значений квадратичной функции \(\displaystyle y=2x^2{\small :}\)
| \(\displaystyle x\) | \(\displaystyle -1\) | \(\displaystyle -0{,}8\) | \(\displaystyle -0{,}6\) | \(\displaystyle -0{,}4\) | \(\displaystyle -0{,}3\) | \(\displaystyle 0\) | \(\displaystyle 0{,}3\) | \(\displaystyle 0{,}4\) | \(\displaystyle 0{,}6\) | \(\displaystyle 0{,}8\) | \(\displaystyle 1\) |
| \(\displaystyle y=2x^2\) | \(\displaystyle 2\cdot (-1)^2\) | \(\displaystyle 2\cdot (-0{,}8)^2\) | \(\displaystyle 2\cdot (-0{,}6)^2\) | \(\displaystyle 2\cdot (-0{,}4)^2\) | \(\displaystyle 2\cdot (-0{,}3)^2\) | \(\displaystyle 0\) | \(\displaystyle 2\cdot 0{,}3^2\) | \(\displaystyle 2\cdot 0{,}4^2\) | \(\displaystyle 2\cdot 0{,}6^2\) | \(\displaystyle 2\cdot 0{,}8^2\) | \(\displaystyle 2\cdot 1^2\) |
Вычислим значения:
| \(\displaystyle x\) | \(\displaystyle -1\) | \(\displaystyle -0{,}8\) | \(\displaystyle -0{,}6\) | \(\displaystyle -0{,}4\) | \(\displaystyle -0{,}3\) | \(\displaystyle 0\) | \(\displaystyle 0{,}3\) | \(\displaystyle 0{,}4\) | \(\displaystyle 0{,}6\) | \(\displaystyle 0{,}8\) | \(\displaystyle 1\) |
| \(\displaystyle \small y=2x^2\) | \(\displaystyle 2\) | \(\displaystyle 1{,}28\) | \(\displaystyle 0{,}72\) | \(\displaystyle 0{,}32\) | \(\displaystyle 0{,}18\) | \(\displaystyle 0\) | \(\displaystyle 0{,}18\) | \(\displaystyle 0{,}32\) | \(\displaystyle 0{,}72\) | \(\displaystyle 1{,}28\) | \(\displaystyle 2\) |
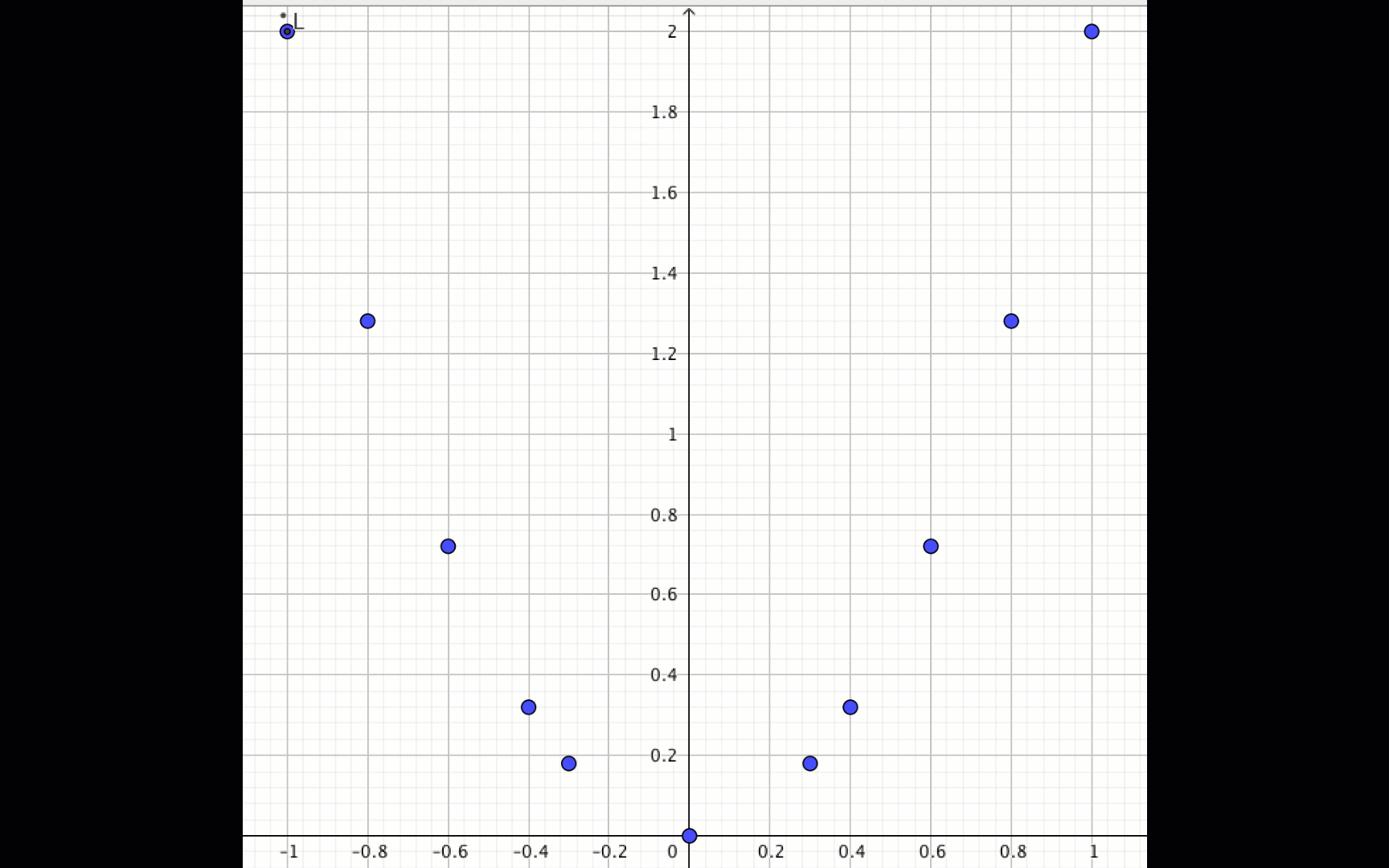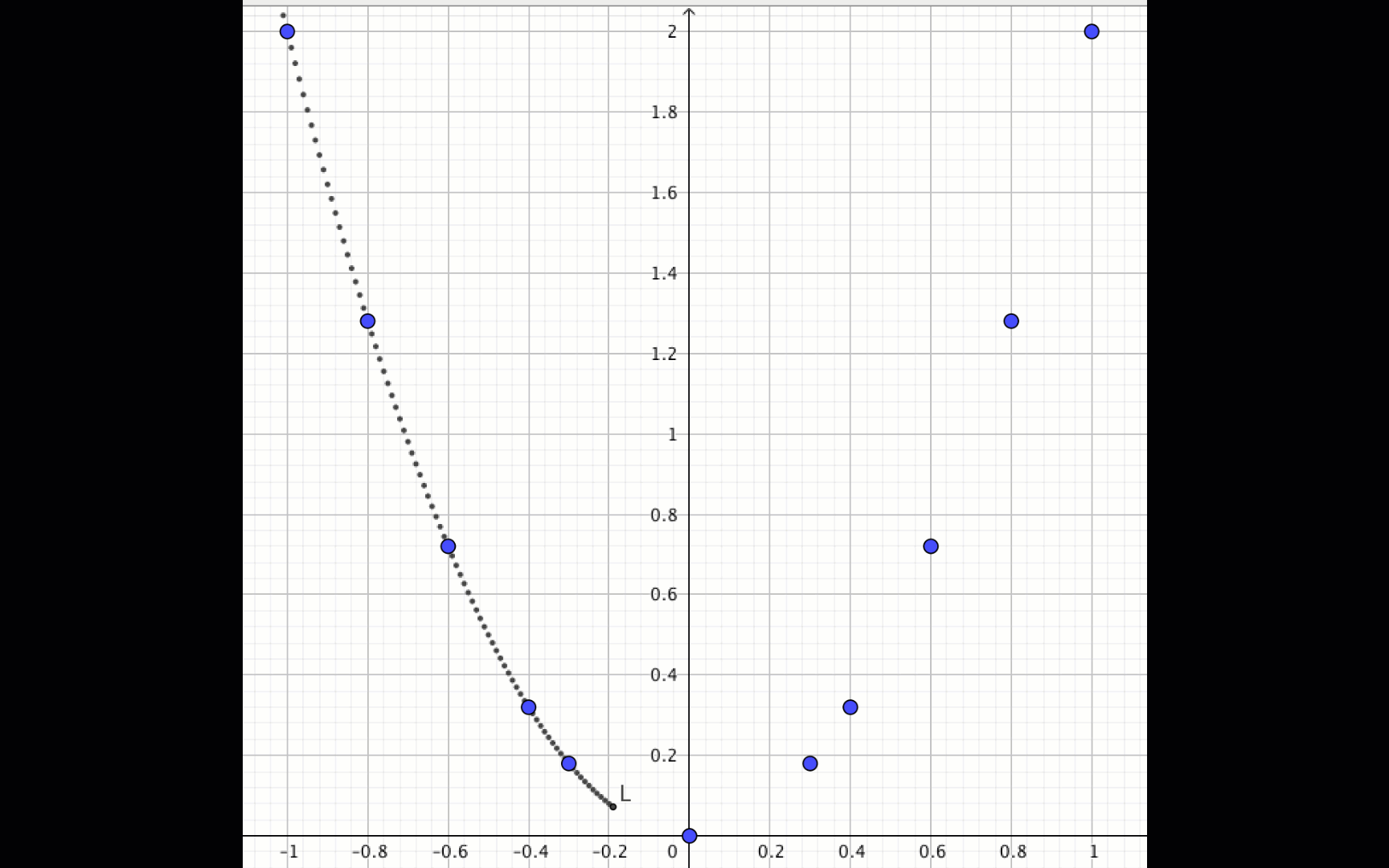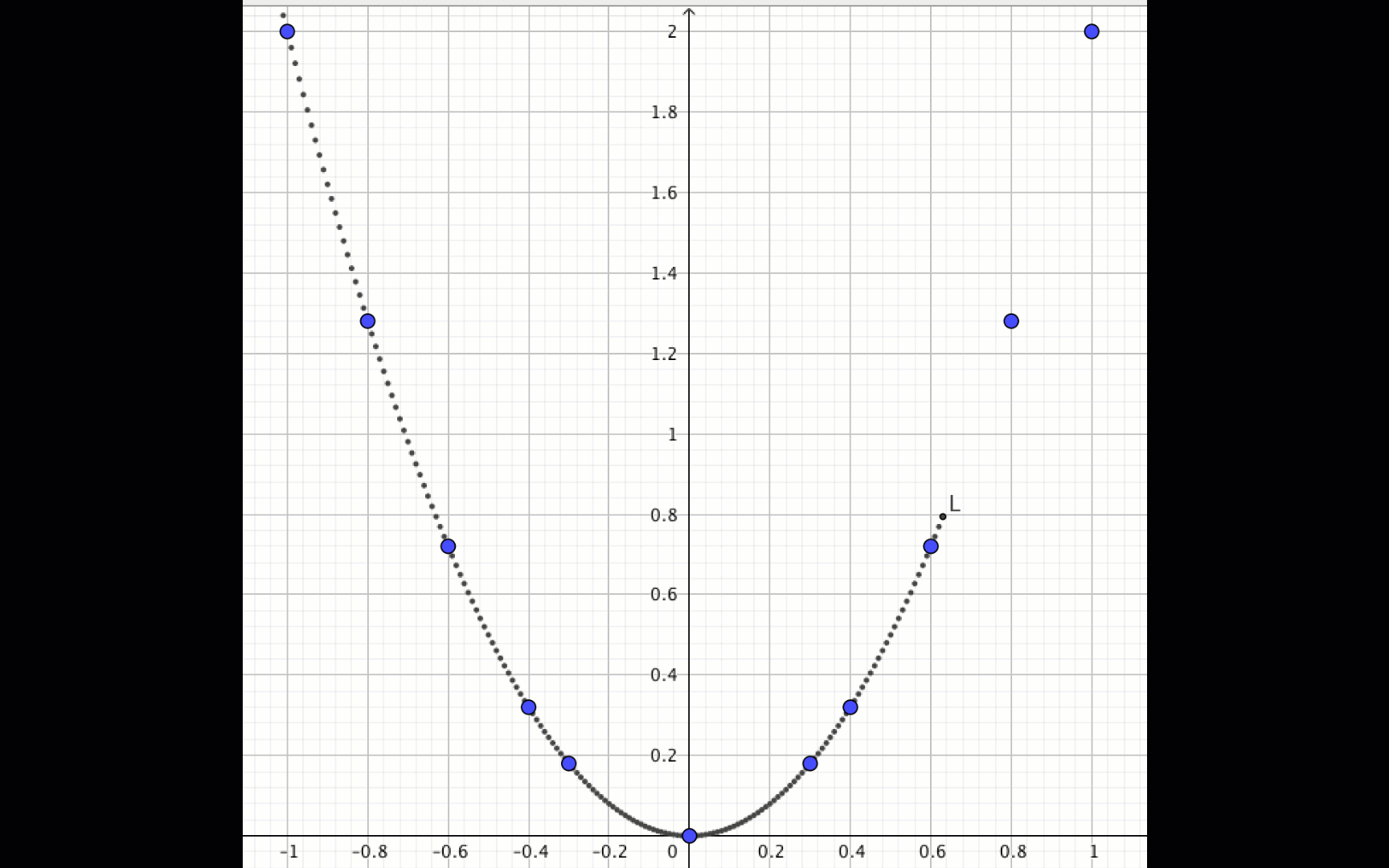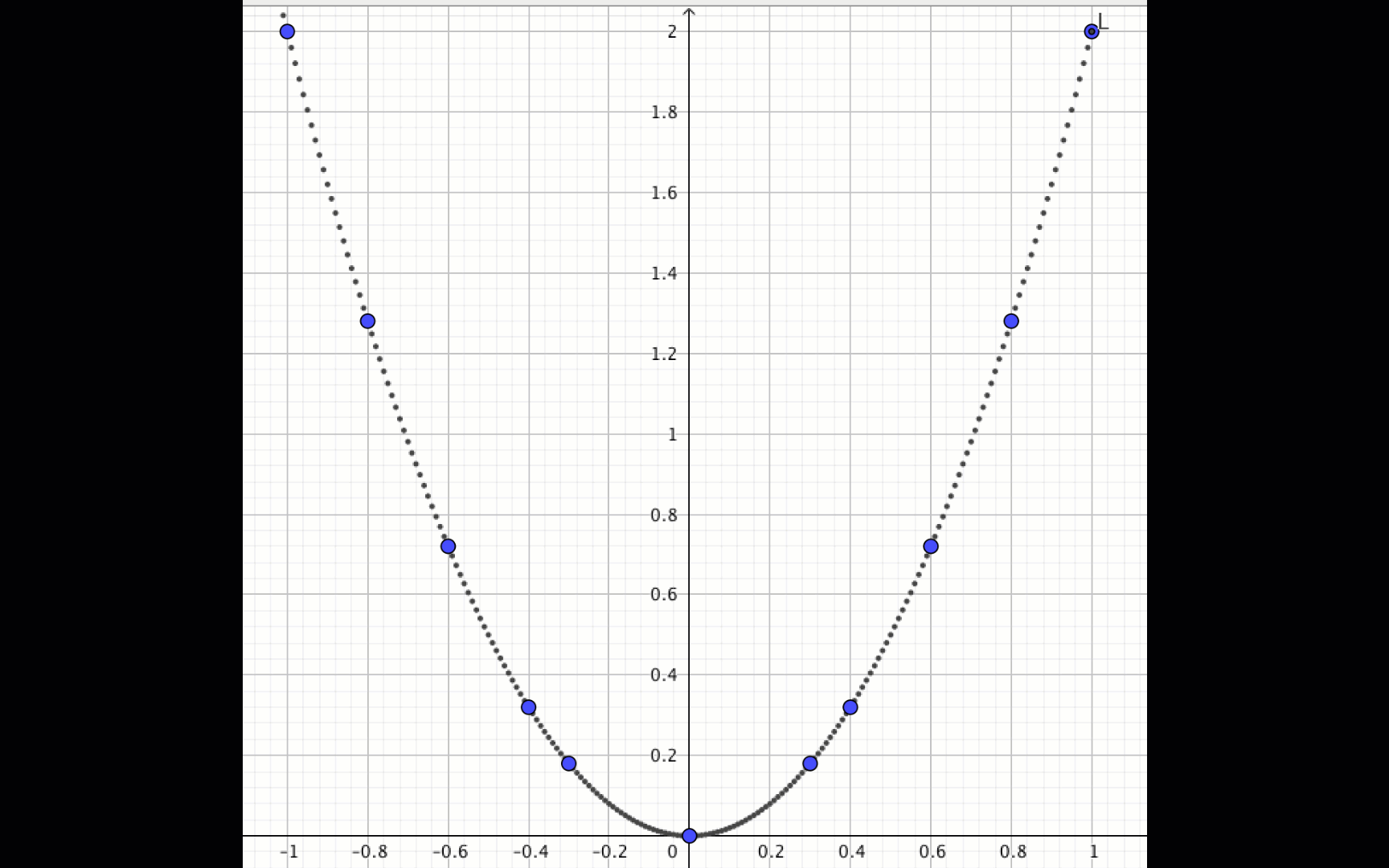
Построим точки на плоскости:
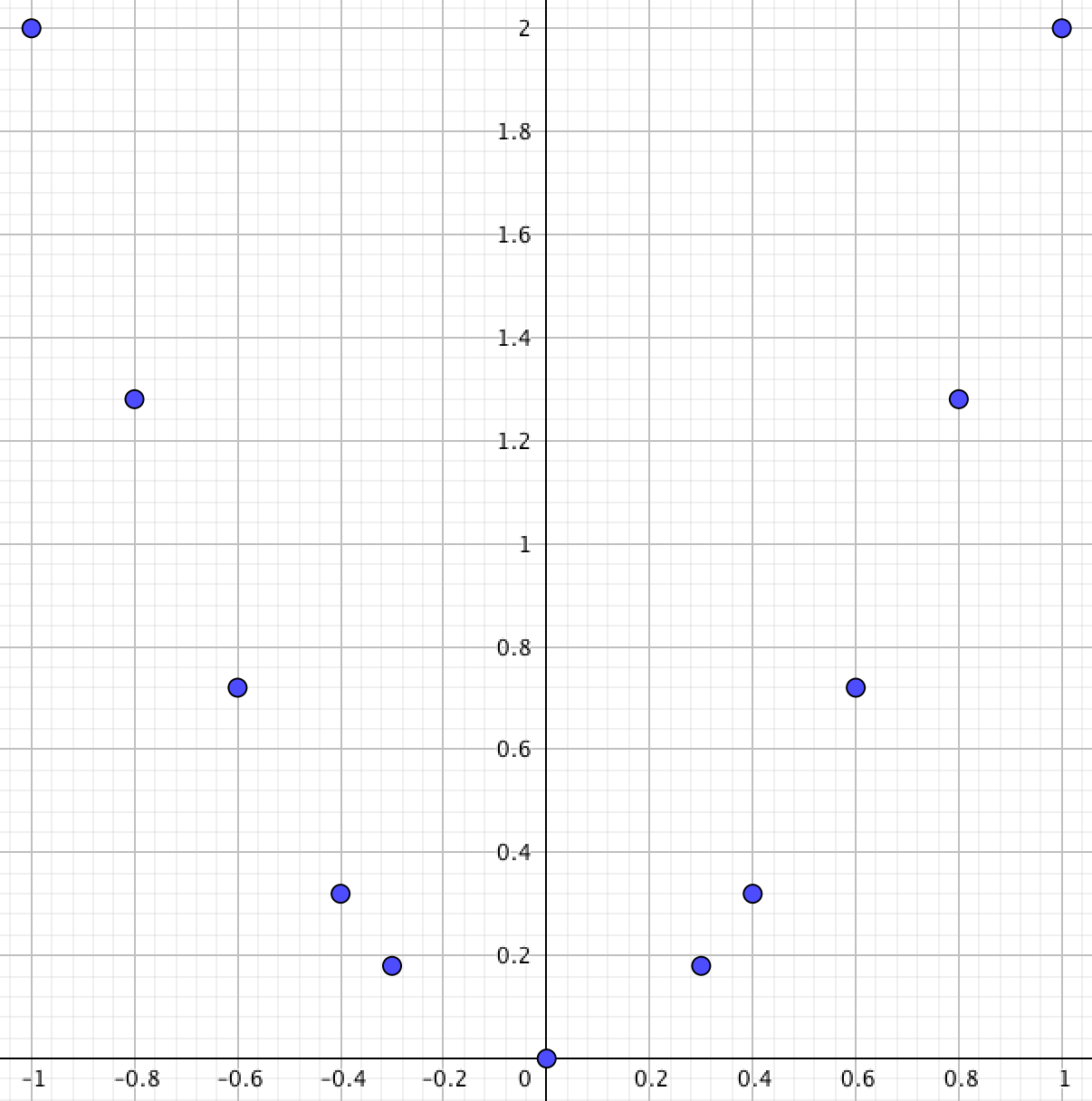
Построим график квадратичной функции \(\displaystyle y=2x^2\) по полученным точкам, добавляя еще точки, если это необходимо:
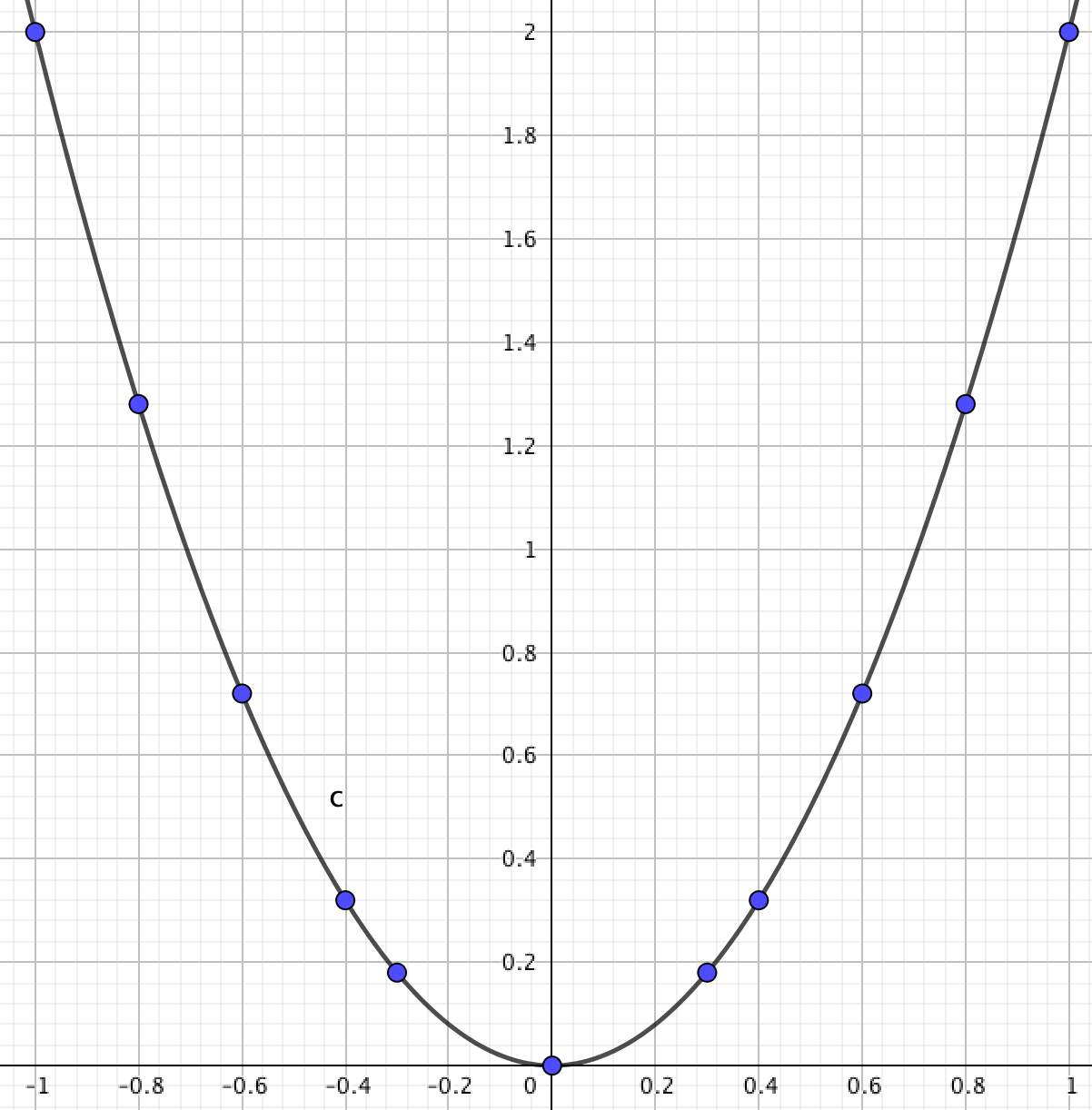
Замечание / комментарий
Построение по точкам
Если построить по оси ОХ много точек с координатами от \(\displaystyle -1 \) до \(\displaystyle 1{\small , } \) то получаем следующую картинку графика: