Тапсырма
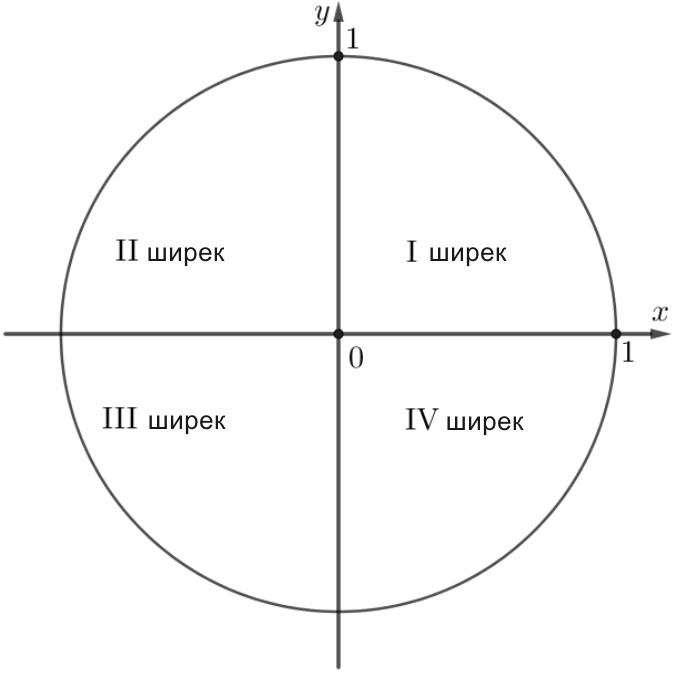
Суретте тангенстің таңбаларын қойып шығыңыз:
- тангенс оң болатын ширектер "\(\displaystyle +\)" белгісімен белгіленеді;
- тангенс теріс болатын ширектер "\(\displaystyle -\)" белгісімен белгіленеді.
Тангенстің таңбалары
Шешім
Тангенстің анықтамасын еске саламыз:
\(\displaystyle \tg(\alpha)=\frac{\sin(\alpha)}{\cos(\alpha)}{\small.}\)
Содан кейін тангенстің таңбаларын анықтау үшін синус пен косинус таңбаларының кестесін еске түсіреміз:
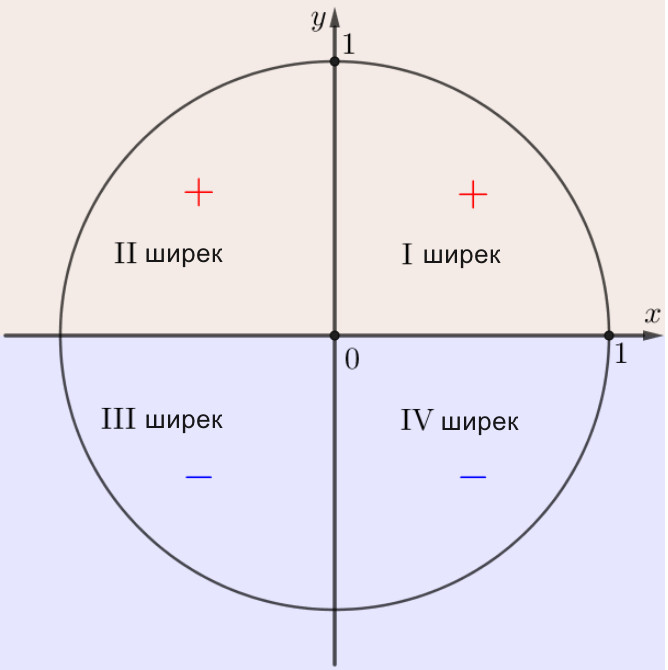
Синус таңбалары
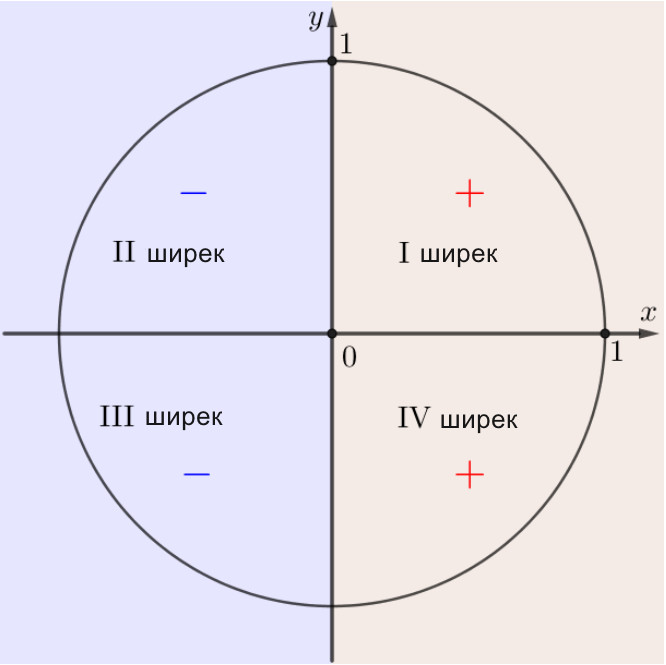
| Косинус таңбалары
|
Сонда
- Бірінші ширекте: \(\displaystyle \sin(\alpha)>0\) және \(\displaystyle \cos(\alpha)>0{\small.}\) Демек, \(\displaystyle \tg(\alpha)=\frac{\sin(\alpha)}{\cos(\alpha)}>0{\small.}\)
- Екінші ширекте: \(\displaystyle \sin(\alpha)>0\) және \(\displaystyle \cos(\alpha)<0{\small.}\) Демек, \(\displaystyle \tg(\alpha)=\frac{\sin(\alpha)}{\cos(\alpha)}<0{\small.}\)
- Үшінші ширекте: \(\displaystyle \sin(\alpha)>0\) және \(\displaystyle \cos(\alpha)<0{\small.}\) Демек, \(\displaystyle \tg(\alpha)=\frac{\sin(\alpha)}{\cos(\alpha)}>0{\small.}\)
- Төртінші ширекте: \(\displaystyle \sin(\alpha)<0\) және \(\displaystyle \cos(\alpha)>0{\small.}\) Демек, \(\displaystyle \tg(\alpha)=\frac{\sin(\alpha)}{\cos(\alpha)}<0{\small.}\)
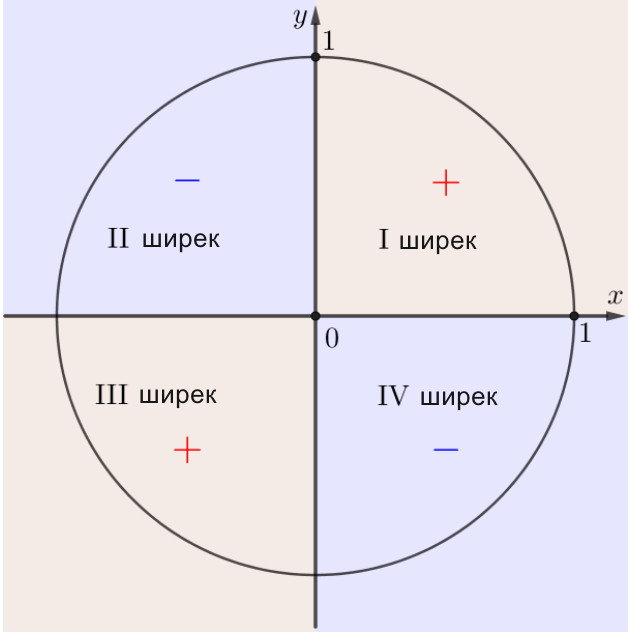
Осылайша, келесіні аламыз:
Тангенс таңбалары