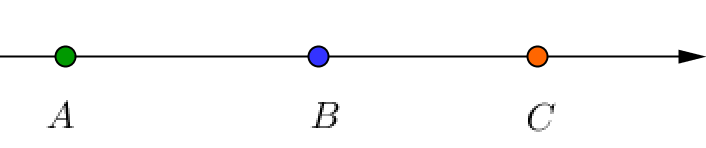
Егер координаттары белгілі болса, түзудегі нүктелердің дұрыс орналасуын таңдаңыз:
\(\displaystyle A\left({\small -2\frac{3}{7}}\right){\small ,}\) \(\displaystyle B(-2{,}7)\) және \(\displaystyle C\left({\small -2\frac{5}{9}}\right){\small .}\)
 | |
 | |
 | |
 |
\(\displaystyle A\left({\small -2\frac{3}{7}}\right){\small ,}\) \(\displaystyle B(-2{,}7)\) және \(\displaystyle C\left({\small -2\frac{5}{9}}\right){\small ,}\) нүктелерінің орнын анықтау үшін, олардың координаттарын салыстырайық:
\(\displaystyle \color{green}{-2\frac{3}{7}}{\small ,}\) \(\displaystyle \color{blue}{-2{,}7}\) және \(\displaystyle \color{orange}{-2\frac{5}{9}}{\small .}\)
Минус таңбаларын алып тастаймыз:
\(\displaystyle \color{green}{2\frac{3}{7}}{\small ,}\) \(\displaystyle \color{blue}{2{,}7}\) және \(\displaystyle \color{orange}{2\frac{5}{9}}{\small ,}\)
алынған оң сандарды салыстырайық.
Алдымен аралас сандар мен ондық бөлшектердің \(\displaystyle 2{\small }\) тең бүтін бөлігі бар екенін ескереміз. Сондықтан бөлшектерді бүтін бөліксіз салыстыру керек:
\(\displaystyle \color{green}{\frac{3}{7}}{\small ,}\) \(\displaystyle \color{blue}{0{,}7}\) и \(\displaystyle \color{orange}{\frac{5}{9}}{\small .}\)
Ол үшін алдымен ондық бөлшекті жай түрге келтірейік \(\displaystyle \color{blue}{0{,}7}=\color{blue}{\frac{7}{10}}{\small , }\)
содан кейін \(\displaystyle \color{green}{\frac{3}{7}},\, \color{blue}{\frac{7}{10}}, \,\color{orange}{\frac{5}{9}}\) бөлшектерін ортақ бөлгішке келтірейік.
\(\displaystyle 7\cdot 10 \cdot 9{\small }\) бөлгіштерінің көбейтіндісіне тең ортақ бөлгішті таңдайық. Сонда
\(\displaystyle \color{green}{\frac{3}{7}}=\color{green}{\frac{3\cdot 10 \cdot 9}{7 \cdot 10 \cdot 9}}=\color{green}{\frac{270}{630}{\small ,}}\)
\(\displaystyle \color{blue}{\frac{7}{10}}=\color{blue}{\frac{7\cdot 7 \cdot 9 }{10 \cdot 7 \cdot 9}}=\color{blue}{\frac{441}{630}}{\small ,}\)
\(\displaystyle \color{orange}{\frac{5}{9}}=\color{orange}{\frac{5 \cdot 7 \cdot 10}{9 \cdot 7 \cdot 10}}=\color{orange}{\frac{350}{630}}{\small .}\)
Төмендегіні аламыз:
\(\displaystyle \color{green}{\frac{270}{630}}<\color{orange}{\frac{350}{630}}<\color{blue}{\frac{441}{630}}{\small ,}\)
\(\displaystyle \color{green}{\frac{3}{7}}<\color{orange}{\frac{5}{9}}<\color{blue}{\frac{7}{10}}=\color{blue}{0{,}7}{\small ,}\)
және
\(\displaystyle \color{green}{2\frac{3}{7}}<\color{orange}{2\frac{5}{9}}<\color{blue}{2{,}7}{\small .}\)
Демек,
\(\displaystyle \color{green}{-2\frac{3}{7}}>\color{orange}{-2\frac{5}{9}}>\color{blue}{-2{,}7}{\small .}\)
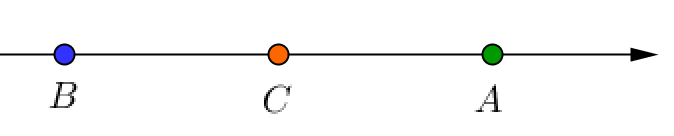
Осылайша, сандық түзудегі \(\displaystyle A\left({\small -2\frac{3}{7}}\right){\small ,}\) \(\displaystyle B(-2{,}7)\) және \(\displaystyle C\left({\small -2\frac{5}{9}}\right)\) нүктелерінің дұрыс орналасуы келесідей:

