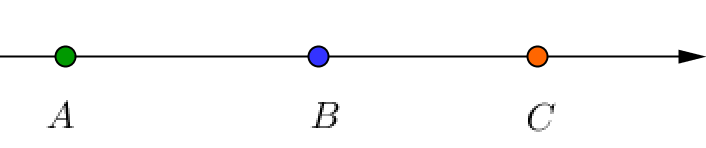
Выберите правильное расположение точек на прямой, если известны их координаты:
\(\displaystyle A\left({\small -2\frac{3}{7}}\right){\small ,}\) \(\displaystyle B(-2{,}7)\) и \(\displaystyle C\left({\small -2\frac{5}{9}}\right){\small .}\)
|
| |
|
| |
 | |
 | |
 | |
 |
Для того чтобы определить положение точек \(\displaystyle A\left({\small -2\frac{3}{7}}\right){\small ,}\) \(\displaystyle B(-2{,}7)\) и \(\displaystyle C\left({\small -2\frac{5}{9}}\right){\small ,}\) сравним их координаты:
\(\displaystyle \color{green}{-2\frac{3}{7}}{\small ,}\) \(\displaystyle \color{blue}{-2{,}7}\) и \(\displaystyle \color{orange}{-2\frac{5}{9}}{\small .}\)
Отбросим знаки минус:
\(\displaystyle \color{green}{2\frac{3}{7}}{\small ,}\) \(\displaystyle \color{blue}{2{,}7}\) и \(\displaystyle \color{orange}{2\frac{5}{9}}{\small ,}\)
и сравним получившиеся положительные числа.
Сначала заметим, что смешанные числа и десятичная дробь имееют одну и ту же целую часть , равную \(\displaystyle 2{\small .}\) Поэтому надо сравнить дроби без целой части:
\(\displaystyle \color{green}{\frac{3}{7}}{\small ,}\) \(\displaystyle \color{blue}{0{,}7}\) и \(\displaystyle \color{orange}{\frac{5}{9}}{\small .}\)
Для этого сначала приведем десятичную дробь к обыкновенному виду \(\displaystyle \color{blue}{0{,}7}=\color{blue}{\frac{7}{10}}{\small , }\)
а затем приведем дроби \(\displaystyle \color{green}{\frac{3}{7}},\, \color{blue}{\frac{7}{10}}, \,\color{orange}{\frac{5}{9}}\) к общему знаменателю.
Выберем общий знаменатель равным произведению знаменателей \(\displaystyle 7\cdot 10 \cdot 9{\small .}\) Тогда
\(\displaystyle \color{green}{\frac{3}{7}}=\color{green}{\frac{3\cdot 10 \cdot 9}{7 \cdot 10 \cdot 9}}=\color{green}{\frac{270}{630}{\small ,}}\)
\(\displaystyle \color{blue}{\frac{7}{10}}=\color{blue}{\frac{7\cdot 7 \cdot 9 }{10 \cdot 7 \cdot 9}}=\color{blue}{\frac{441}{630}}{\small ,}\)
\(\displaystyle \color{orange}{\frac{5}{9}}=\color{orange}{\frac{5 \cdot 7 \cdot 10}{9 \cdot 7 \cdot 10}}=\color{orange}{\frac{350}{630}}{\small .}\)
Получаем:
\(\displaystyle \color{green}{\frac{270}{630}}<\color{orange}{\frac{350}{630}}<\color{blue}{\frac{441}{630}}{\small ,}\)
\(\displaystyle \color{green}{\frac{3}{7}}<\color{orange}{\frac{5}{9}}<\color{blue}{\frac{7}{10}}=\color{blue}{0{,}7}{\small ,}\)
и
\(\displaystyle \color{green}{2\frac{3}{7}}<\color{orange}{2\frac{5}{9}}<\color{blue}{2{,}7}{\small .}\)
Значит,
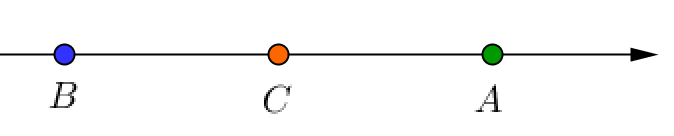
\(\displaystyle \color{green}{-2\frac{3}{7}}>\color{orange}{-2\frac{5}{9}}>\color{blue}{-2{,}7}{\small .}\)
Таким образом, верное расположение точек \(\displaystyle A\left({\small -2\frac{3}{7}}\right){\small ,}\) \(\displaystyle B(-2{,}7)\) и \(\displaystyle C\left({\small -2\frac{5}{9}}\right)\) на числовой прямой имеет вид:

