По условию задачи даны сторона основания \(\displaystyle BC=16\) и площадь боковой поверхности \(\displaystyle S_{бок}=360 {\small .}\) 

Требуется найти боковое ребро \(\displaystyle SC\) пирамиды.

Боковые грани правильной пирамиды – равные треугольники. Следовательно, площади боковых граней равны.

У правильной треугольной пирамиды три боковых грани. Значит,

\(\displaystyle S_{бок}=S_{грани}+S_{грани}+S_{грани}=3S_{грани}\small. \)

Тогда 

\(\displaystyle 360=3S_{грани}\small, \)

\(\displaystyle S_{грани}=120\small. \)

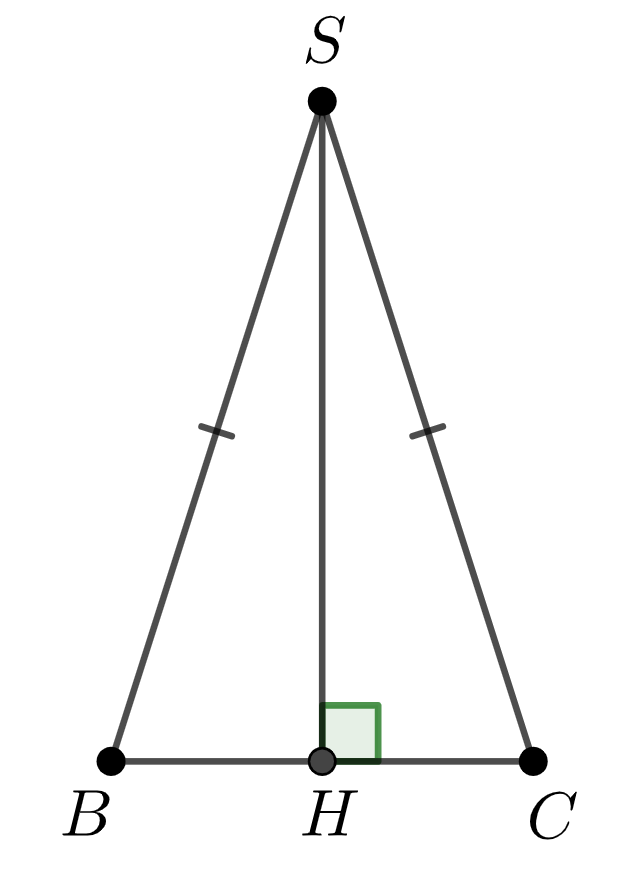
Проведем высоту \(\displaystyle SH\) в грани \(\displaystyle SBC{\small :}\)

Площадь треугольника равна половине произведения высоты на сторону, к которой она проведена. То есть

\(\displaystyle S_{грани}=\frac{1}{2}BC\cdot SH{\small .}\)

Найдем \(\displaystyle SH{\small :}\)

\(\displaystyle 120=\frac{1}{2}\cdot 16 \cdot SH{\small ,}\)

\(\displaystyle 120=8 \cdot SH{\small ,}\)

\(\displaystyle SH=15{\small .}\)

Отрезок \(\displaystyle SH\) является высотой равнобедренного треугольника \(\displaystyle SBC{\small ,}\) проведенной к основанию \(\displaystyle BC{\small .}\)

Следовательно, \(\displaystyle SH\) также является медианой треугольника \(\displaystyle SBC{\small .}\) 

Значит,

\(\displaystyle BH=HC=\frac{1}{2}BC=\frac{1}{2}\cdot 16 = 8{\small .}\)

Рассмотрим прямоугольный треугольник \(\displaystyle SHC{\small .}\)

Найдем \(\displaystyle SC\) по теореме Пифагора для треугольника \(\displaystyle SHC{\small :}\) \(\displaystyle SH^2+HC^2=SC^2{\small ,}\) \(\displaystyle SC^2=15^2+{17}^2{\small ,}\) \(\displaystyle SC^2=289{\small .}\) Так как \(\displaystyle SC\) – длина отрезка, то \(\displaystyle SC>0\), и, следовательно, \(\displaystyle SC=\sqrt{289}=17{\small .}\)

Ответ: \(\displaystyle 17{\small .}\)