Найдите значение выражения:
\(\displaystyle \sqrt{3}\cos^2 {\frac{5\pi}{12}} -\sqrt{3} \sin^2 {\frac{5\pi}{12}}=\)
В данной разности \(\displaystyle \sqrt{3}\cos^2 {\frac{5\pi}{12}} -\sqrt{3} \sin^2 {\frac{5\pi}{12}}\) есть общий множитель \(\displaystyle \sqrt{3}{\small.}\) Вынесем его за скобку:
\(\displaystyle \sqrt{3}\cos^2 {\frac{5\pi}{12}} -\sqrt{3} \sin^2 {\frac{5\pi}{12}}=\sqrt{3}\,(\cos^2 {\frac{5\pi}{12}} -\sin^2 {\frac{5\pi}{12}}) {\small.}\)
В скобках получилась разность квадратов косинуса и синуса.
При этом как синус, так и косинус имеют один и тот же угол \(\displaystyle \frac{5\pi}{12}.\)
Значит, можно применить формулу косинуса двойного угла:
\(\displaystyle \cos\, 2\color{red}{\alpha}=\cos^2\color{red}{\alpha}-\sin^2\color{red}{\alpha}\)
В нашем случае \(\displaystyle \alpha=\frac{5\pi}{12},\) то есть
\(\displaystyle \cos^2 \color{red}{\frac{5\pi}{12}}-\sin^2 \color{red}{\frac{5\pi}{12}}=\cos(2 \cdot \color{red}{\frac{5\pi}{12}})\)
и так как \(\displaystyle 2 \cdot \frac{5\pi}{12}=\frac{5\pi}{6},\) то
\(\displaystyle \cos^2 \frac{5\pi}{12}-\sin^2 \frac{5\pi}{12}=\cos \frac{5\pi}{6}{\small.}\)
Тогда:
\(\displaystyle \sqrt{3}\,(\cos^2 {\frac{5\pi}{12}} -\sin^2 {\frac{5\pi}{12}}) =\sqrt{3} \cos \frac{5\pi}{6} {\small.}\)
Найдём, чему равен \(\displaystyle \cos \frac{5\pi}{6} {\small.}\)
\(\displaystyle \frac{5\pi}{6}=\pi-\frac{\pi}{6}{\small .}\)
Тогда
\(\displaystyle \cos \frac{5\pi}{6} =\cos (\pi-\frac{\pi}{6}){\small .}\)
Применим формулу приведения по правилу:
1) Определяем четверть, в которой находится угол.
2) Определяем знак исходной функции.
3) Определяем, какая функция будет
Если к углу \(\displaystyle \pm \alpha \) добавляем или вычитаем
- \(\displaystyle \pm\pi ,\, \pm 2\pi ,\, \pm 3\pi,\, \pm 4\pi,\,\ldots\) (целое число \(\displaystyle \pi\)), то функцию не меняем;
- \(\displaystyle \pm\frac{\pi}{2},\, \pm\frac{3\pi}{2},\, \pm\frac{5\pi}{2},\, \pm\frac{7\pi}{2},\, \ldots\) (нечетное число половинок \(\displaystyle \pi\)), то функцию меняем: \(\displaystyle \sin\) \(\displaystyle \leftrightarrow\) \(\displaystyle \cos\) и \(\displaystyle \tg\) \(\displaystyle \leftrightarrow\) \(\displaystyle \ctg\).
1. Определим, в какой четверти находится угол \(\displaystyle \pi-\frac{\pi}{6}{:}\)
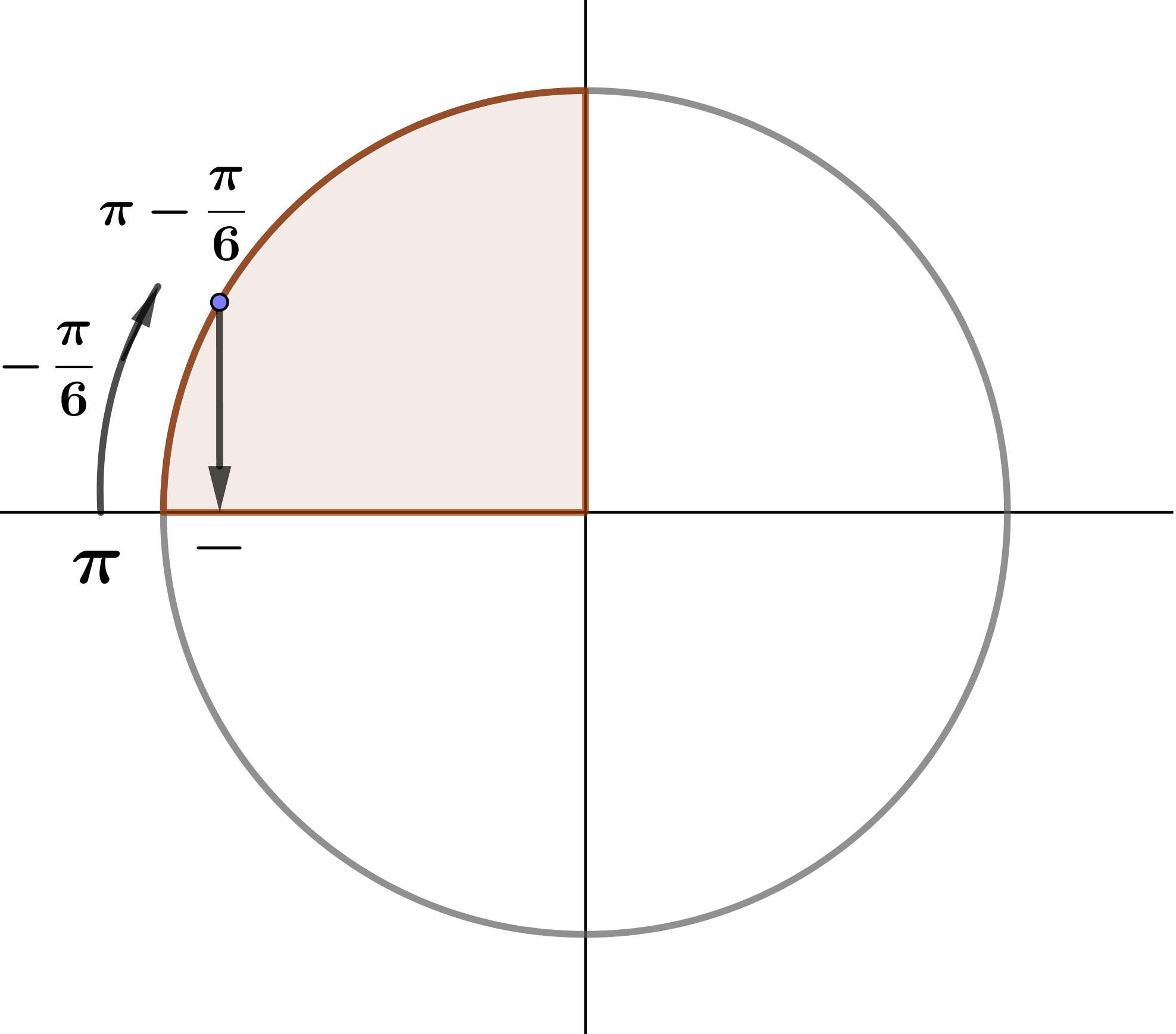
Значит, угол \(\displaystyle \pi-\frac{\pi}{6} \) находится во второй четверти.
2. Определим знак исходной функции.
Во второй четверти косинус отрицательный (\(\displaystyle {\bf -}\)).
3. Определим, какая будет функция.
Так как к аргументу \(\displaystyle -\frac{\pi}{6}\) прибавляем \(\displaystyle \pi ,\) то функция не меняется.
Значит,
\(\displaystyle \cos {(\pi-\frac{\pi}{6})}=-\cos {\frac{\pi}{6}} {\small ,}\)
то есть \(\displaystyle \cos \frac{5\pi}{6}=-\cos {\frac{\pi}{6}} {\small .}\)
Тогда:
\(\displaystyle \sqrt{3} \cos \frac{5\pi}{6}=-\sqrt{3} \cos \frac{\pi}{6}{\small .}\)
Подставим табличное значение.
\(\displaystyle - \sqrt{3} \cos \frac{\pi}{6}=-\sqrt{3} \cdot \frac{\sqrt{3}}{2}=-\frac{3}{2}=-1{,}5{\small.}\)
Таким образом, верна следующая цепочка равенств:
\(\displaystyle \sqrt{3}\cos^2 {\frac{5\pi}{12}} -\sqrt{3} \sin^2 {\frac{5\pi}{12}}=\sqrt{3}\,(\cos^2 {\frac{5\pi}{12}} -\sin^2 {\frac{5\pi}{12}})=\sqrt{3} \cos \frac{5\pi}{6}=-\sqrt{3} \cos \frac{\pi}{6}=-\sqrt{3} \cdot \frac{\sqrt{3}}{2}=-1{,}5{\small.}\)
Ответ: \(\displaystyle -1{,}5 {\small.} \)
