Если \(\displaystyle \color{blue}{ k}>1{ \small ,}\) то для ненулевого \(\displaystyle x_0\) точка с координатами \(\displaystyle \color{blue}{ (x_0;\,-kx_0^2)} \) лежит ниже точки с координатами \(\displaystyle \color{green}{ (x_0; -x_0^2)}{ \small ,} \) так как \(\displaystyle \color{blue}{ -kx_0^2}<\color{green}{ -x_0^2}{\small .}\)

Таким образом, ВСЕ точки вида \(\displaystyle \color{blue}{ (x_0;\,-kx_0^2)} \) (кроме точки \(\displaystyle (0;0)\)) лежат ниже точек с координатами вида \(\displaystyle \color{green}{ (x_0; -x_0^2)}{ \small :} \)

Все точки вида  \(\displaystyle \color{blue}{ (x_0;\,-kx_0^2)} \) – это парабола \(\displaystyle y=\color{blue}{ -kx^2}{\small .}\)

Все точки вида  \(\displaystyle \color{green}{ (x_0; -x_0^2)}\) – это парабола \(\displaystyle y=\color{green}{ -x^2}{\small .}\)

Следовательно, график квадратичной функции \(\displaystyle y=\color{blue}{ -kx^2}\) лежит ниже параболы \(\displaystyle y=\color{green}{ -x^2}{\small :}\)

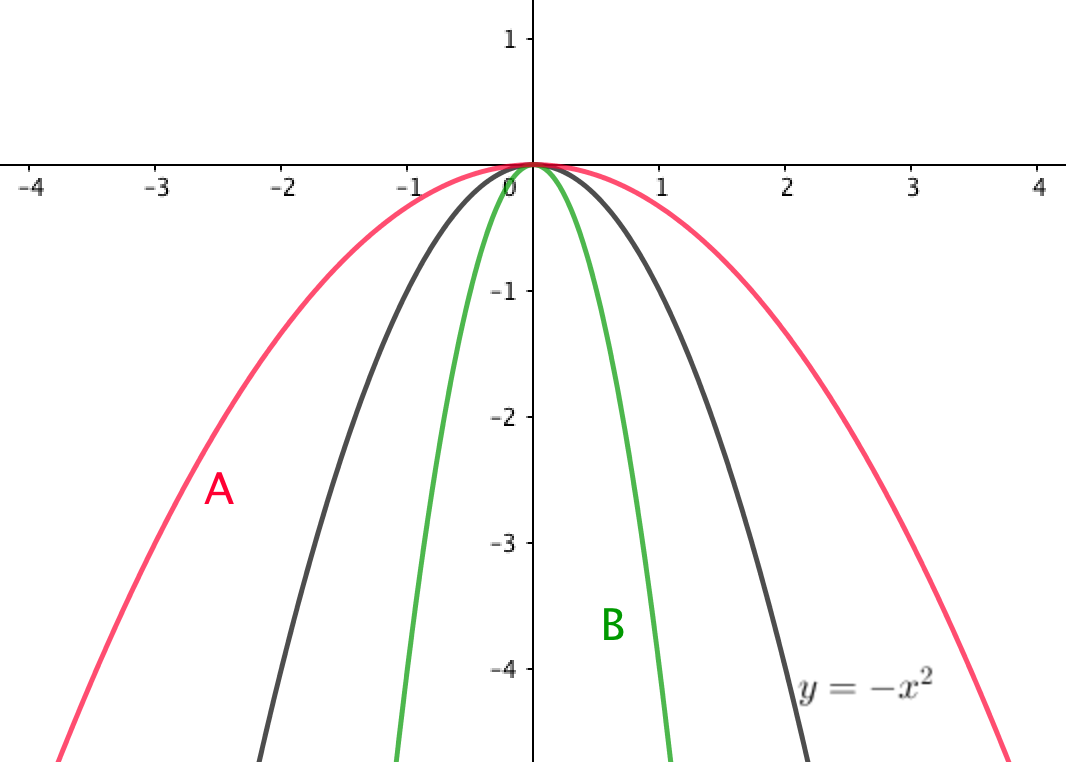
Посмотрим на рисунок, данный в условии:

Поскольку график параболы \(\displaystyle y=-kx^2\) лежит ниже графика параболы \(\displaystyle y=-x^2{ \small ,} \) то верный ответ \(\displaystyle \color{green}{\rm B}{\small .} \)