\(\displaystyle A(5;\, 6){\small }\) нүктесі арқылы өтетін түзудің теңдеуін табыңыз, егер ол \(\displaystyle y=kx-4{\small }\) түрінің сызықтық функциясымен берілетіні белгілі болса.
\(\displaystyle y=\)\(\displaystyle x-4\)
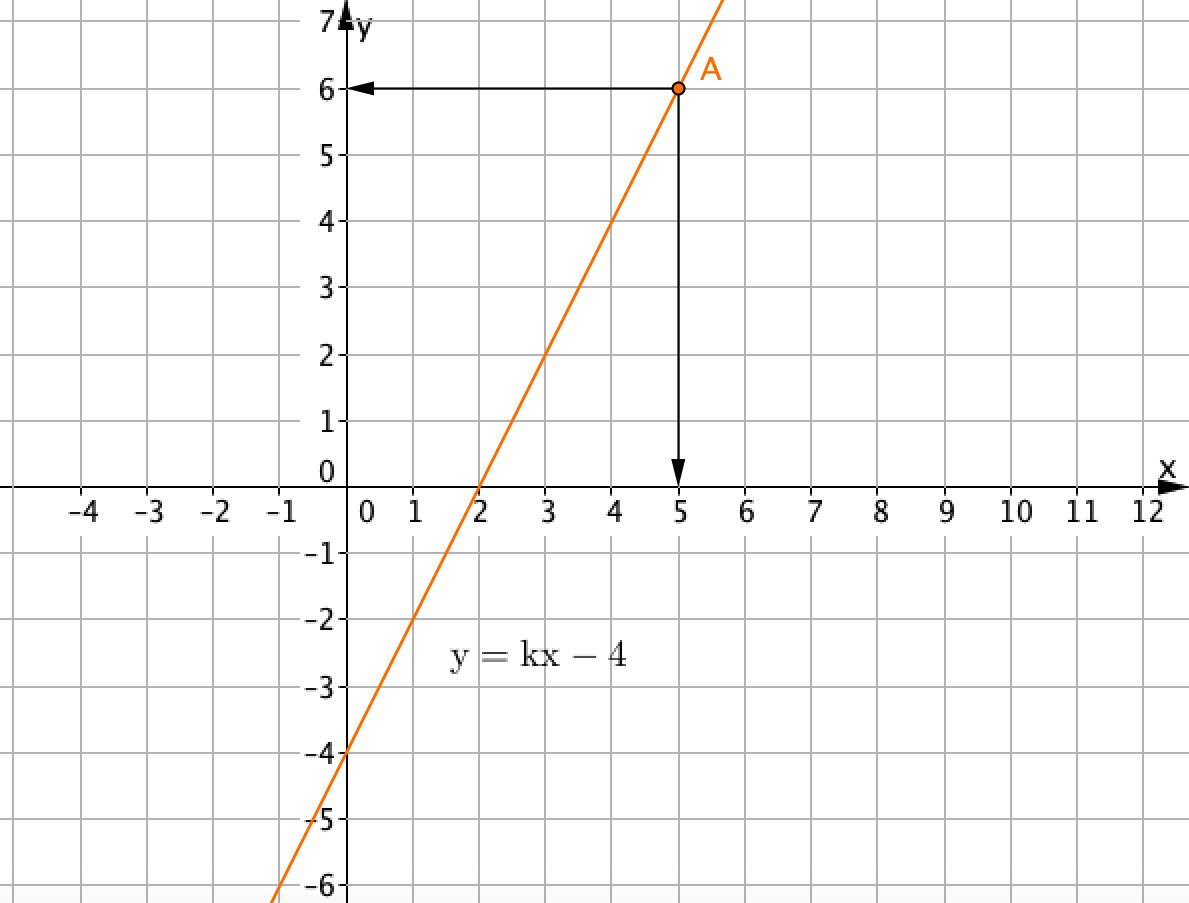
\(\displaystyle y=kx-4\) түзуі \(\displaystyle A(\color{blue}{5};\, \color{green}{6}){\small }\) нүктесі арқылы өтетіні белгілі . Бұл дегеніміз, егер берілген нүктенің координаттарын теңдеуге алмастырсақ, онда біз дұрыс теңдікке ие боламыз.
\(\displaystyle A(\color{blue}{5};\, \color{green}{6})\) нүктесінің координаттарын \(\displaystyle y=kx-4\,{\small }\) түзуінің теңдеуіне алмастырайық :
\(\displaystyle \color{green}{6}=k\cdot \color{blue}{5}-4{\small .}\)
\(\displaystyle k\,{\small } \) мәнін табайық:
\(\displaystyle 6=5k-4{\small ;}\)
\(\displaystyle k=\frac{6+4}{5}=\frac{10}{5}=2{\small .}\)
Жауабы: \(\displaystyle y={\bf 2}x-4{\small . } \)
