Найдите уравнение прямой, проходящей через точку \(\displaystyle A(-2;\, -3){\small ,}\) если известно, что она задается линейной функцией вида \(\displaystyle y=x+b\) для некоторого отрицательного числа \(\displaystyle b{\small . } \)
\(\displaystyle y=x\,\,\)
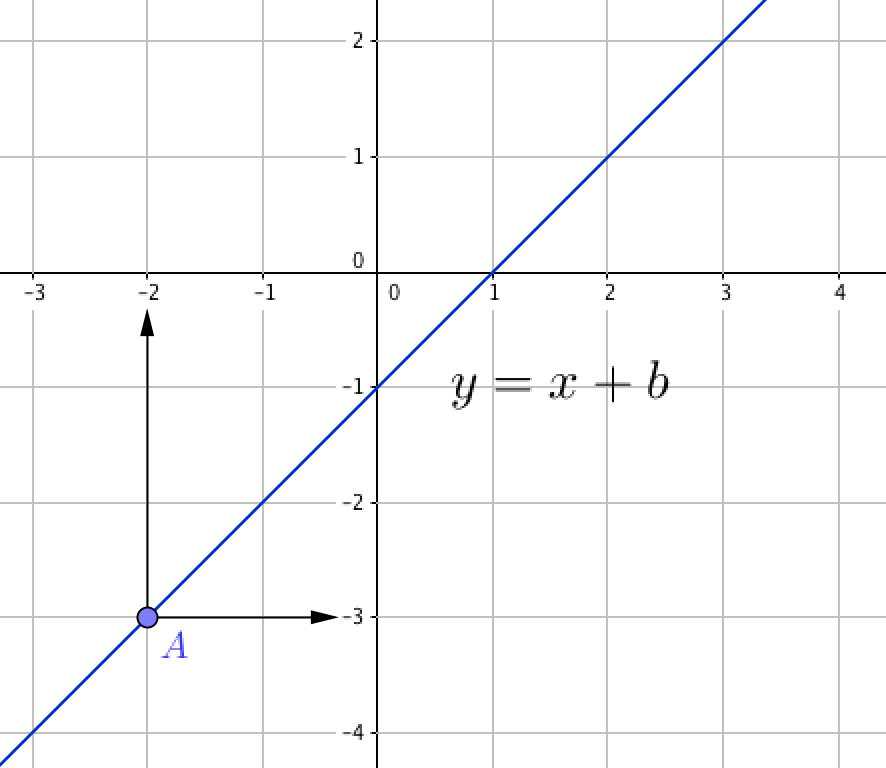
Известно, что прямая \(\displaystyle y=x+b\) проходит через точку \(\displaystyle A(\color{blue}{ -2};\, \color{green}{ -3}){\small .}\) Это означает, что если подставить координаты данной точки в уравнение, то мы получим верное равенство.
Подставим координаты точки \(\displaystyle A(\color{blue}{ -2};\, \color{green}{ -3})\) в уравнение прямой \(\displaystyle y=x+b\,{\small :}\)
\(\displaystyle \color{green}{ -3}=\color{blue}{ -2}+b{\small .}\)
Найдем значение \(\displaystyle b\,{\small : } \)
\(\displaystyle b=2-3=-1{\small .}\)
Ответ: \(\displaystyle y=x-{\bf 1}{\small . } \)
