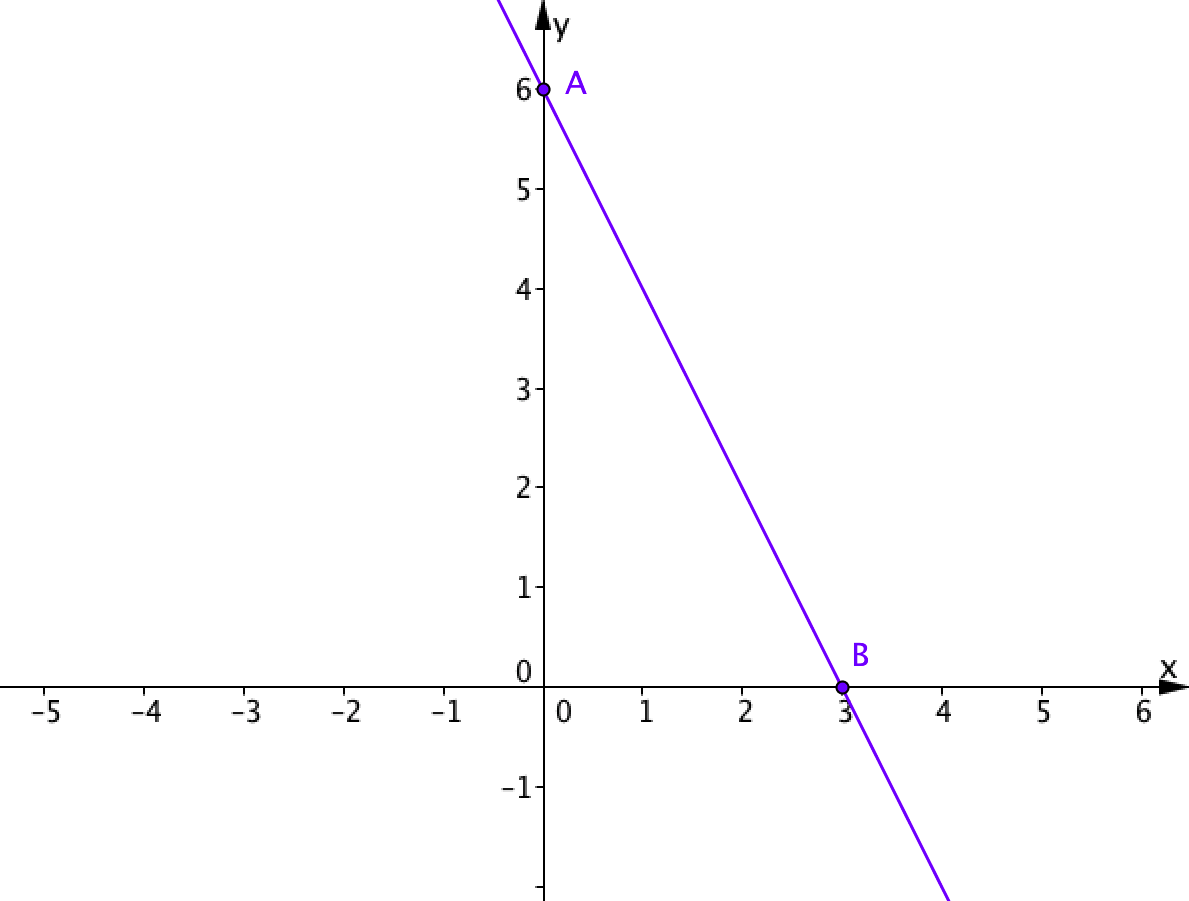
Найдите уравнение прямой, проходящей через точки \(\displaystyle A(0;\, 6)\) и \(\displaystyle B(3;\, 0){\small .}\)
\(\displaystyle y=\)
Поскольку прямая \(\displaystyle y=kx+b\) проходит через точки \(\displaystyle A(0;\, 6)\) и \(\displaystyle B(3;\, 0){\small ,}\) то это означает, что координаты этих точек удовлетворяют уравнению прямой.
Подставим координаты точек в уравнение прямой \(\displaystyle y=kx+b\,{\small : }\)
1) для точки \(\displaystyle A(\color{blue}{ 0};\color{green}{ 6}){\small : }\)
\(\displaystyle 6=k\cdot \color{blue}{ 0}+b \,{\small ; }\)
2) для точки \(\displaystyle B(\color{blue}{ 3};\color{green}{ 0}){\small : }\)
\(\displaystyle \color{green}{ 0}=k\cdot \color{blue}{ 3}+b {\small . }\)
Запишем эти два уравнения вместе:
\(\displaystyle \begin{aligned}6=&k\cdot 0+b{\small ,}\\0=&k\cdot 3+b{\small .}\end{aligned}\)
Из первого уравнения легко находится \(\displaystyle b\,{\small : } \)
\(\displaystyle 6=0+b \,{\small ; }\)
\(\displaystyle b=6{\small . }\)
Подставим это значение \(\displaystyle \color{green}{b=6}\) во второе уравнение \(\displaystyle 0=k\cdot 3+\color{green}{b}\,{\small : } \)
\(\displaystyle 0=k\cdot 3+\color{green}{6}{\small , } \)
\(\displaystyle 0=3k+\color{green}{6}{\small . }\)
Теперь можно найти \(\displaystyle k\,{\small : } \)
\(\displaystyle -3k=6 {\small ; }\)
\(\displaystyle k=6:(-3) {\small ; }\)
\(\displaystyle k=-2 {\small . }\)
Таким образом, подставляя в уравнение \(\displaystyle y=kx+b\) получившиеся значения для \(\displaystyle k \) и \(\displaystyle b{\small , } \) получаем:
\(\displaystyle y=-2x+6{\small . } \)
Ответ: \(\displaystyle y=-2x+6{\small . }\)
