Выберите уравнения, задающие прямую.
Прямая задается
- либо уравнением \(\displaystyle y=kx+b{\small ,}\) для некоторых чисел \(\displaystyle k,\, b\) (то есть является графиком линейной функции),
- либо уравнением \(\displaystyle x=a{\small ,}\) для некоторого числа \(\displaystyle a{\small .}\)
\(\displaystyle {\bf y=\frac{3}{x}}\)
Так как
- \(\displaystyle y=\frac{3}{x}\) не линейная функция (выражение \(\displaystyle \frac{3}{x}\) не является многочленом первой степени),
- это не прямая, заданная уравнением \(\displaystyle x=a{\small ,}\) для некоторого числа \(\displaystyle a{\small ,}\)
то прямая не является графиком функции \(\displaystyle y=\frac{3}{x}{\small .}\)
Кроме того, если поточечно начертить график функции \(\displaystyle y=\frac{3}{x}{\small ,}\) то получим:
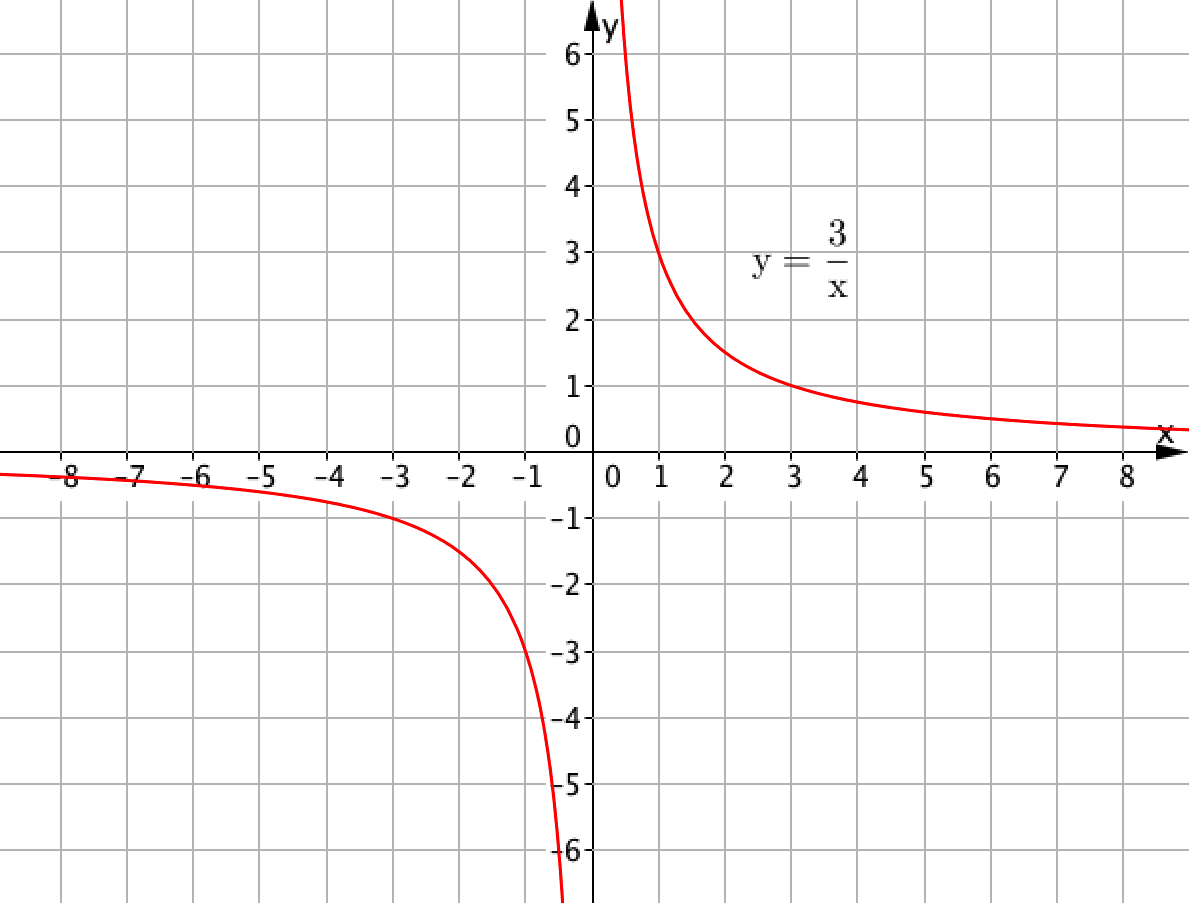
Это не прямая.
\(\displaystyle {\bf y=\frac{1}{x-2}}\)
Так как
- \(\displaystyle y=\frac{1}{x-2}\) не линейная функция (выражение \(\displaystyle \frac{1}{x-2}\) не является многочленом первой степени),
- это не прямая, заданная уравнением \(\displaystyle x=a{\small ,}\) для некоторого числа \(\displaystyle a{\small ,}\)
то прямая не является графиком функции \(\displaystyle y=\frac{1}{x-2}{\small .}\)
Кроме того, если поточечно начертить график функции \(\displaystyle y=\frac{1}{x-2}{\small ,}\) то получим:
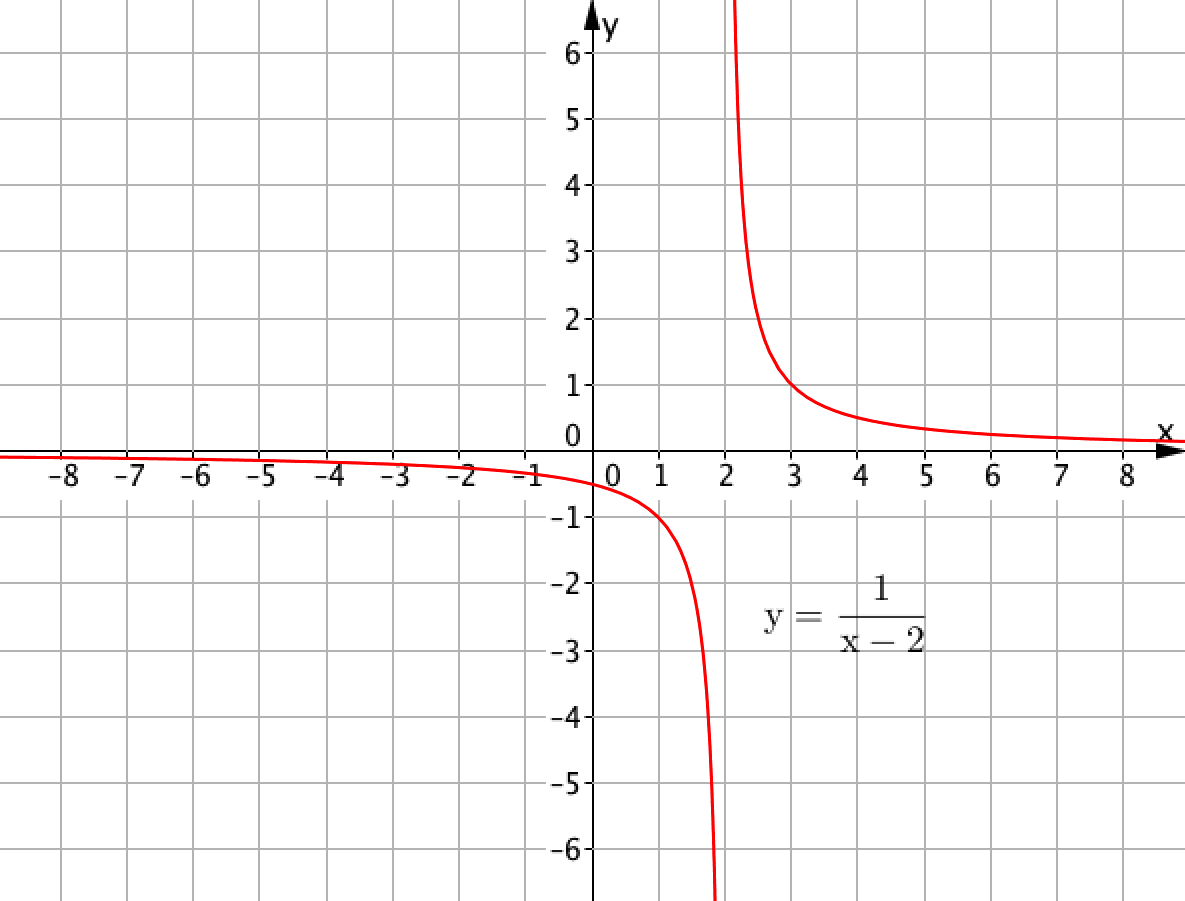
Это не прямая.
\(\displaystyle {\bf y=3x-1}\)
Так как \(\displaystyle y=15x-21\) является линейной функцией, то графиком данной функции является прямая.
Кроме того, если начертить график функции \(\displaystyle y=3x-1{\small ,}\) то получим:
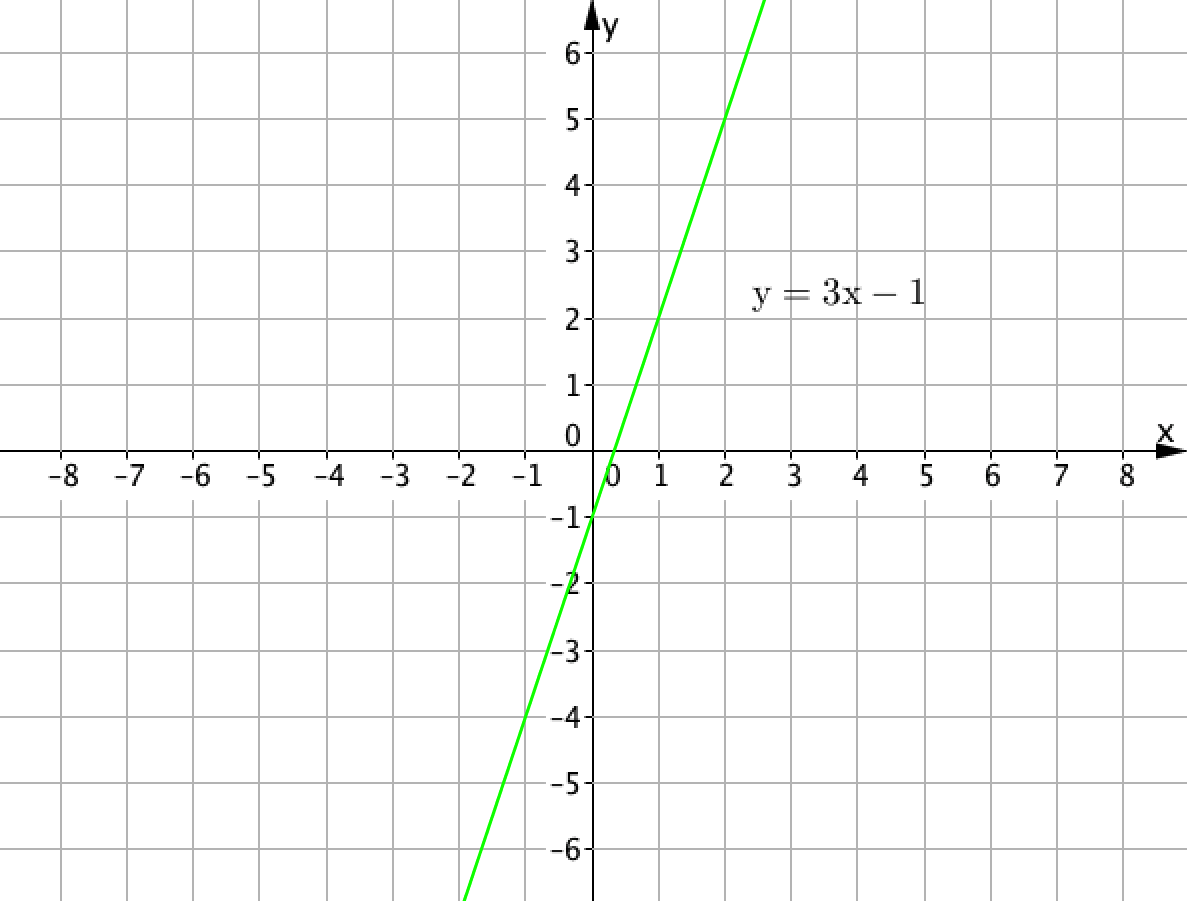
Это прямая.
\(\displaystyle {\bf y=x^{\,3}+2}\)
Так как
- \(\displaystyle y=x^{\,3}+2\) не линейная функция (выражение \(\displaystyle x^{\,3}+2\) многочлен третьей степени),
- это не прямая, заданная уравнением \(\displaystyle x=a{\small ,}\) для некоторого числа \(\displaystyle a{\small ,}\)
то прямая не является графиком функции \(\displaystyle y=x^{\,3}+2{\small .}\)
Кроме того, если поточечно начертить график функции \(\displaystyle y=x^{\,3}+2{\small ,}\) то получим:
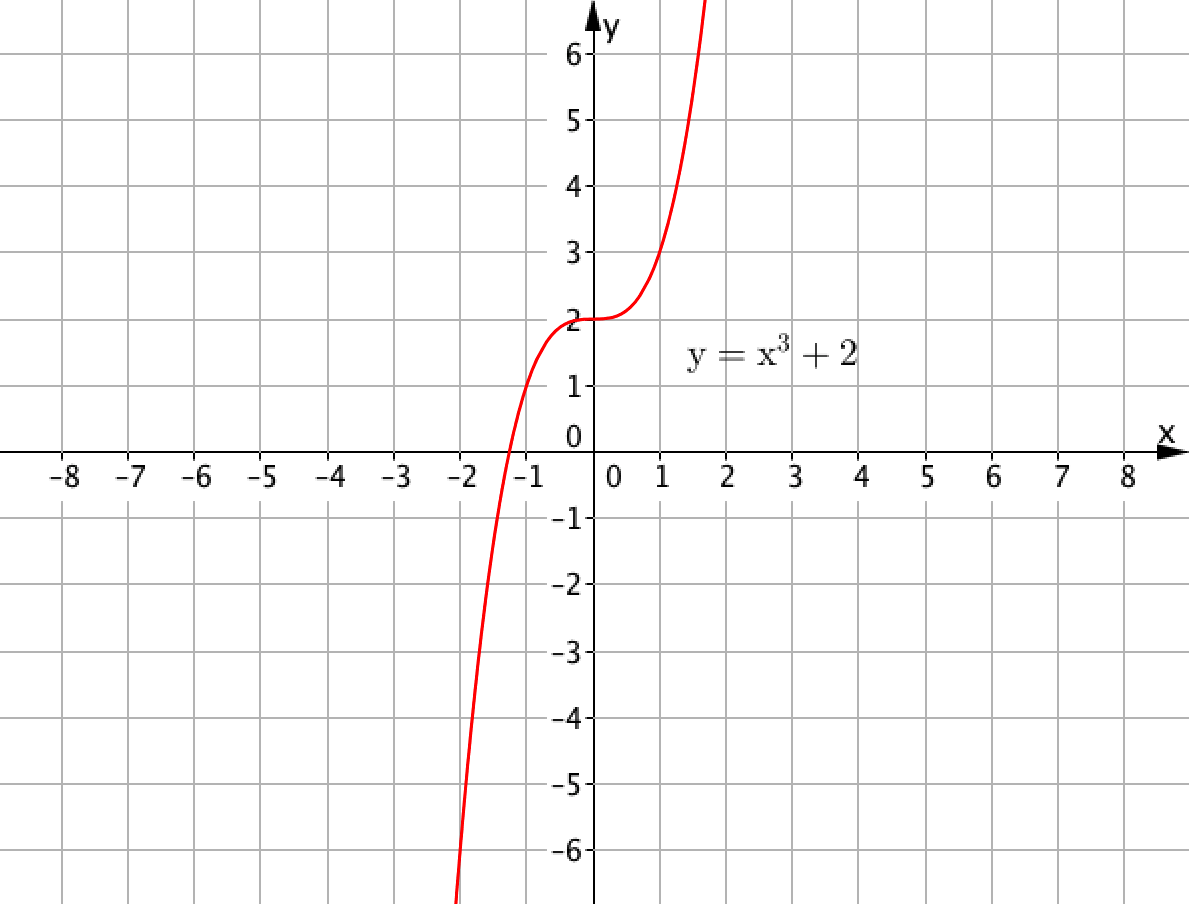
Это не прямая.
\(\displaystyle {\bf x=-7}\)
Из правила следует, что \(\displaystyle x=-7\) задает прямую.
Кроме того, если поточечно начертить график \(\displaystyle x=-7{\small ,}\) то получим:
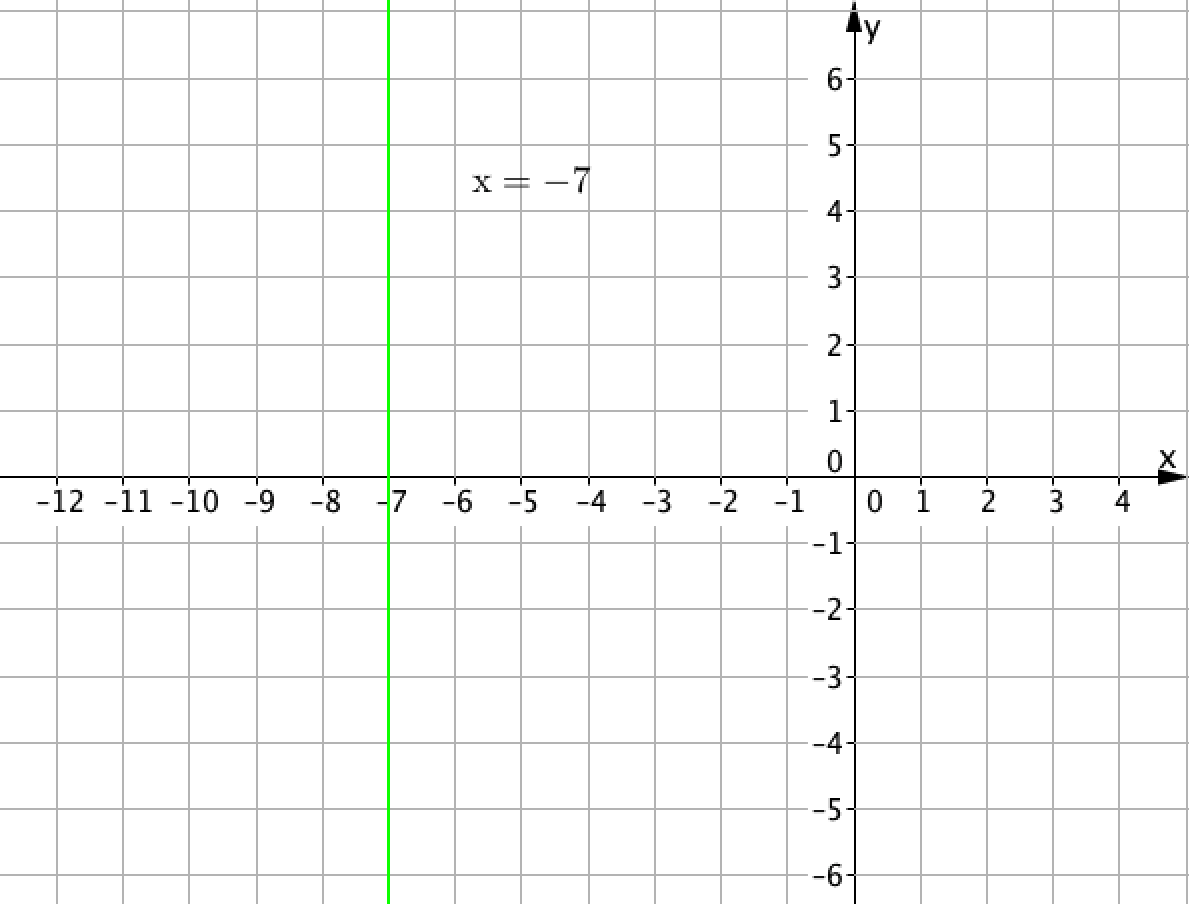
Это прямая.
