Түзуді беретін теңдеулерді таңдаңыз.
Түзу беріледі
- не кейбір \(\displaystyle k,\, b\) сандары үшін \(\displaystyle y=kx+b{\small }\) теңдеуімен (яғни сызықтық функцияның графигі болып табылады),
- не кейбір \(\displaystyle a{\small }\) саны үшін \(\displaystyle x=a{\small }\) теңдеуімен .
\(\displaystyle {\bf y=\frac{3}{x}}\)
\(\displaystyle y=\frac{3}{x}\) сызықтық функция емес болғандықтан (\(\displaystyle \frac{3}{x}\) өрнегі бірінші дәрежелі көпмүше болып табылмайды),
- бұл кейбір \(\displaystyle a{\small }\) саны үшін \(\displaystyle x=a{\small }\) теңдеуімен берілген түзу емес болғандықтан ,
онда түзу \(\displaystyle y=\frac{3}{x}{\small }\) функциясының графигі болып табылмайды.
Сонымен қатар, егер \(\displaystyle y=\frac{3}{x}{\small }\) функциясының графигін нүктелеп сызсақ, онда келесіні аламыз:
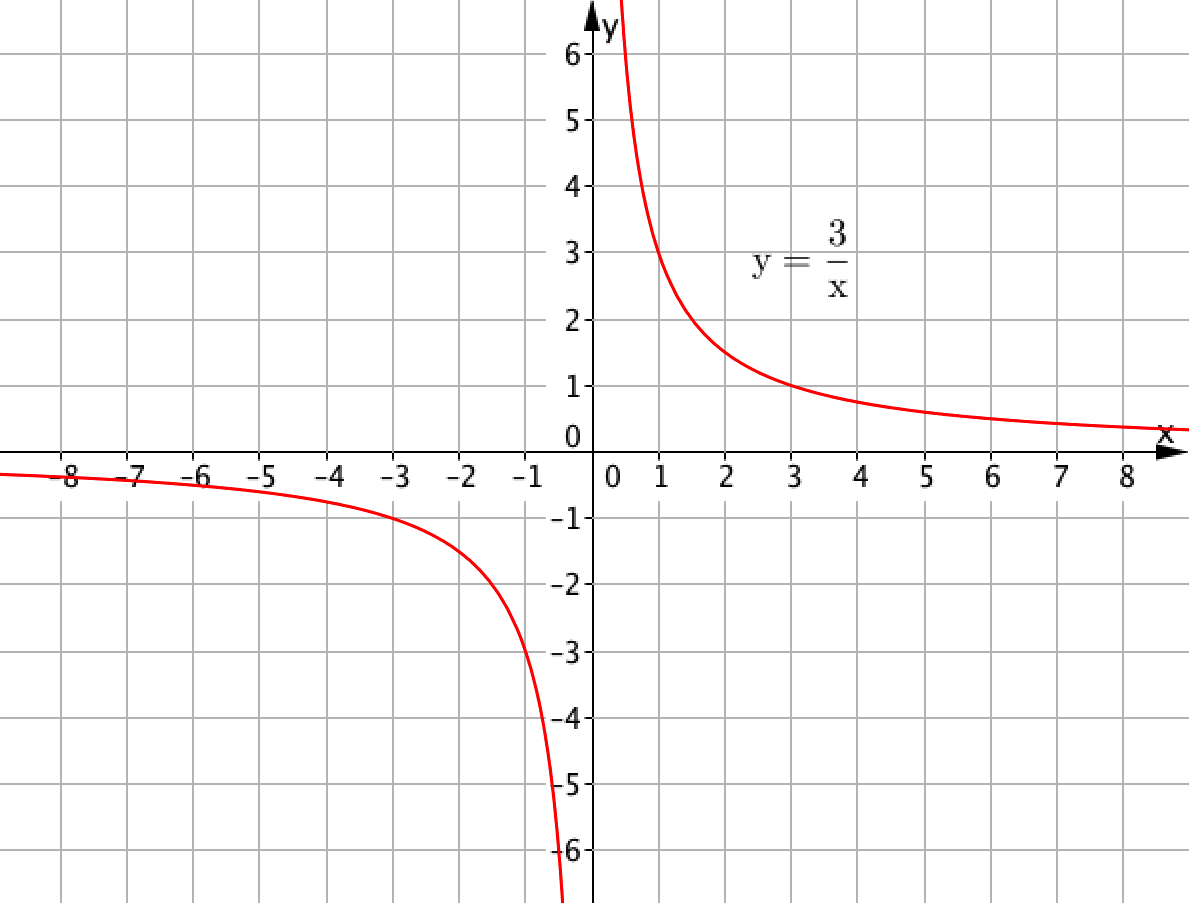
Бұл түзу емес.
\(\displaystyle {\bf y=\frac{1}{x-2}}\)
- \(\displaystyle y=\frac{1}{x-2}\) сызықтық функция емес болғандықтан (\(\displaystyle \frac{1}{x-2}\) өрнегі бірінші дәрежелі көпмүше болып табылмайды),
- бұл кейбір \(\displaystyle a{\small }\) саны үшін \(\displaystyle x=a{\small }\) теңдеуімен берілген түзу емес болғандықтан ,
онда түзу \(\displaystyle y=\frac{1}{x-2}{\small }\) функциясының графигі болып табылмайды.
Сонымен қатар, егер \(\displaystyle y=\frac{1}{x-2}{\small }\) функциясының графигін нүктелеп сызсақ, онда келесіні аламыз:
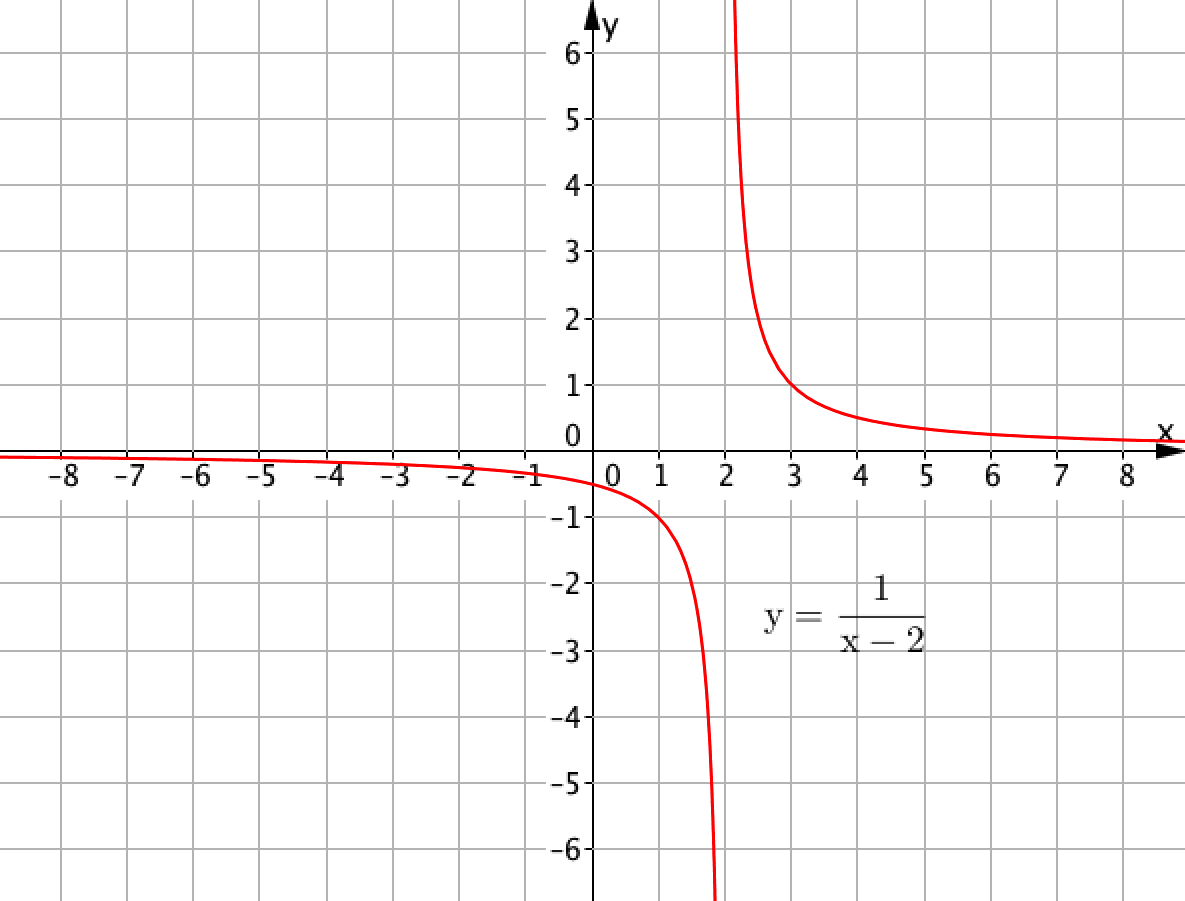
Бұл түзу емес.
\(\displaystyle {\bf y=3x-1}\)
\(\displaystyle y=15x-21\) сызықтық функция болып табылатындықтан, онда бұл функцияның графигі түзу болып табылады.
Сонымен қатар, егер \(\displaystyle y=3x-1{\small }\) функциясының графигін сызсақ, онда келесіні аламыз:
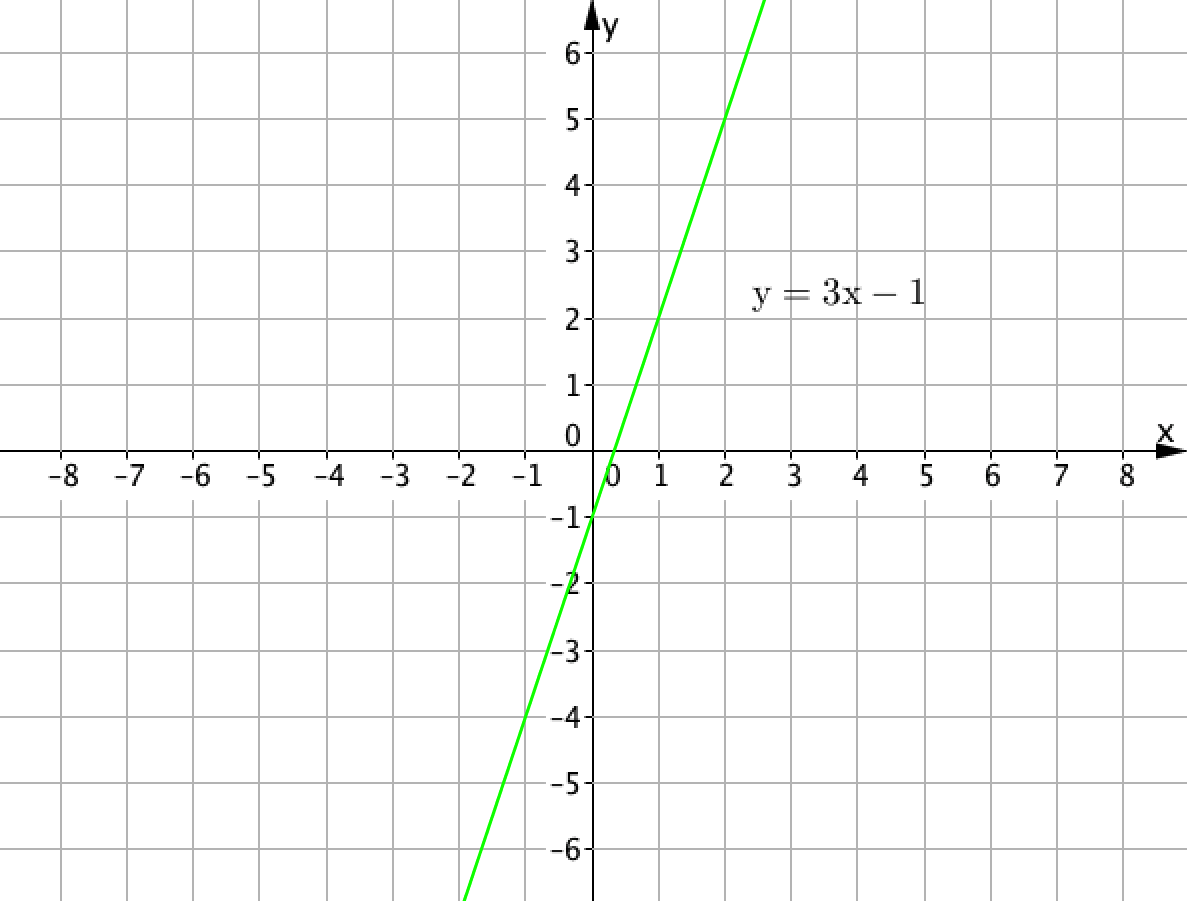
Бұл түзу.
\(\displaystyle {\bf y=x^{\,3}+2}\)
Так как
- \(\displaystyle y=x^{\,3}+2\) сызықтық функция емес болғандықтан ( \(\displaystyle x^{\,3}+2\) өрнегі үшінші дәрежелі көпмүше),
- бұл кейбір \(\displaystyle a{\small }\) саны үшін \(\displaystyle x=a{\small }\) теңдеуімен берілген түзу емес болғандықтан ,
онда түзу \(\displaystyle y=x^{\,3}+2{\small }\) функциясының графигі болып табылмайды.
Сонымен қатар, егер \(\displaystyle y=x^{\,3}+2{\small ,}\) функциясының графигін нүктелеп сызсақ, онда келесіні аламыз:
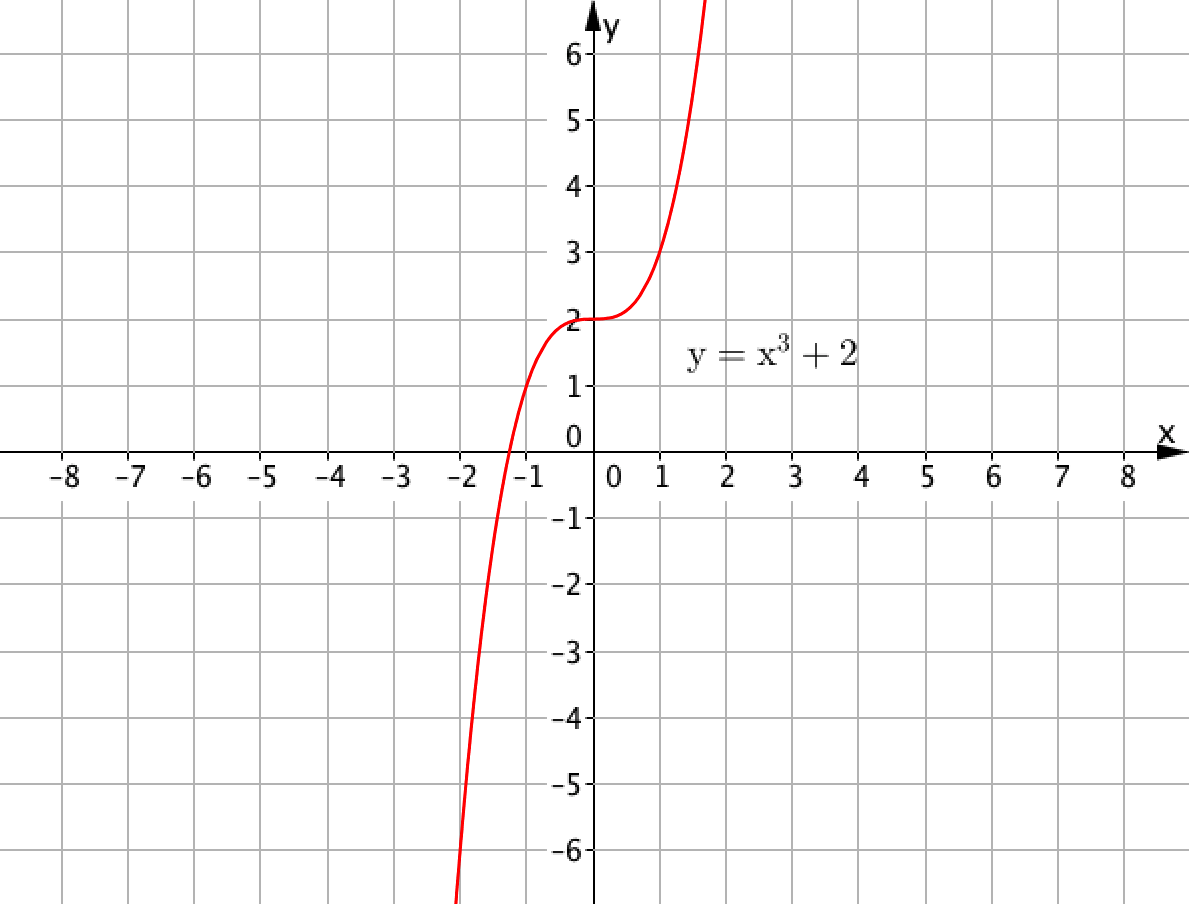
Бұл түзу емес.
\(\displaystyle {\bf x=-7}\)
Ережеден \(\displaystyle x=-7\) түзуді беретіні шығады.
Сонымен қатар, егер \(\displaystyle x=-7{\small ,}\) графигін нүктелеп сызсақ , онда келесіні аламыз:
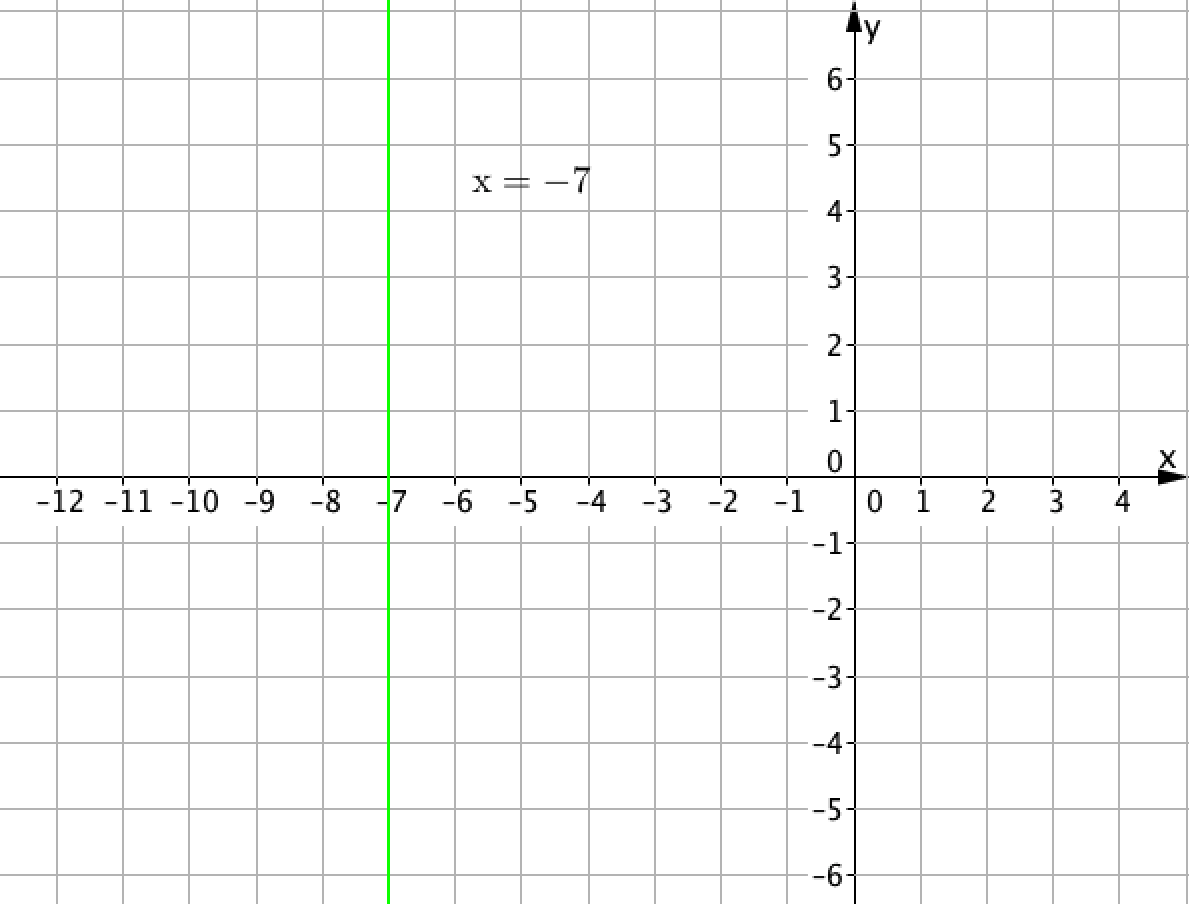
Бұл түзу.
