Дана парабола \(\displaystyle y=x^2{\small .}\) Найдите координаты точек \(\displaystyle A\) и \(\displaystyle B\,{\small :}\)
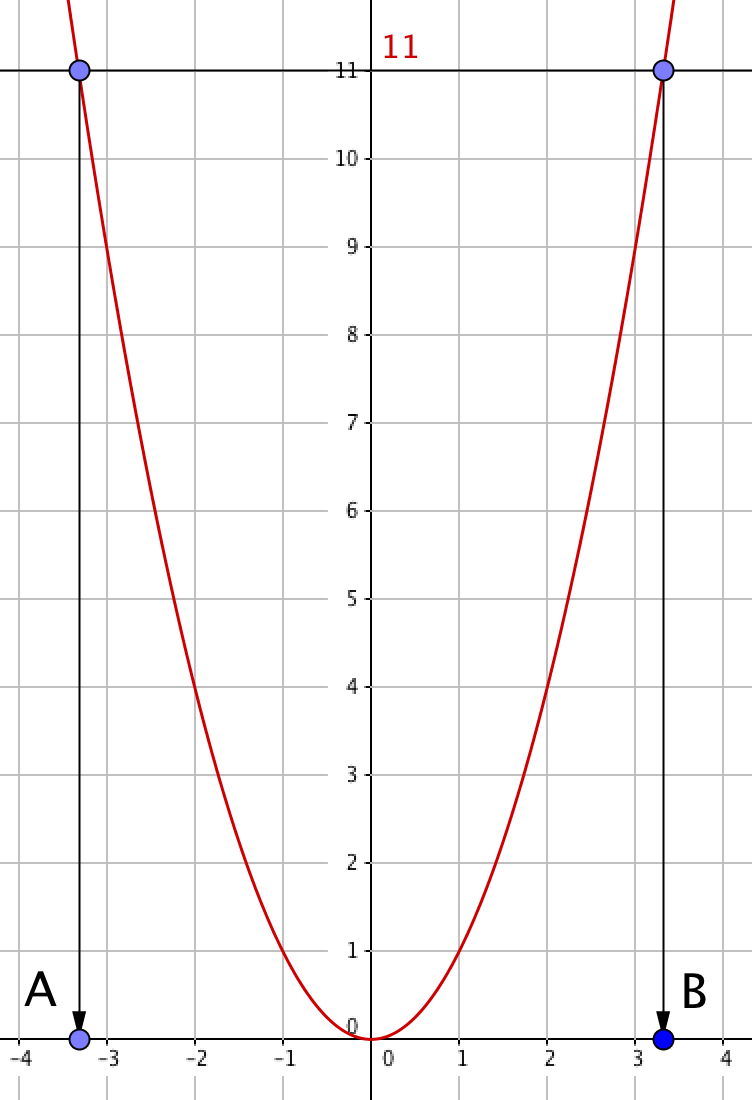
Пусть \(\displaystyle {\rm C} \) и \(\displaystyle {\rm D}\) – точки на параболе \(\displaystyle y=x^2 {\small ,}\) которые проецируются на точки\(\displaystyle {\rm A} \) и \(\displaystyle {\rm B} \) соответственно:
Точка \(\displaystyle {\rm A} \) имеет ту же координату по оси \(\displaystyle OX{\small , } \) что и точка \(\displaystyle {\rm C}{\small ,} \) а точка \(\displaystyle {\rm B} \) – ту же, что и точка \(\displaystyle {\rm D}{\small .} \)
Поэтому найдем координаты по оси \(\displaystyle OX \) для точек \(\displaystyle {\rm C} \) и \(\displaystyle {\rm D}{\small . } \)
Из рисунка видно, что точки \(\displaystyle {\rm C} \) и \(\displaystyle {\rm D} \) имеют по оси \(\displaystyle OY \) координату \(\displaystyle 11{\small . } \) Тогда их координаты имеют вид
\(\displaystyle {\rm C}(x\,;11) \) и \(\displaystyle {\rm D}(x\,;11){\small . } \)
С другой стороны, координаты этих точек удовлетворяют уравнению параболы \(\displaystyle y=x^2{\small , } \) на которой они лежат. Так как в нашем случае \(\displaystyle y=11{\small , } \) то
\(\displaystyle 11=x^2{\small , }\)
где \(\displaystyle x \) – это координаты точек \(\displaystyle {\rm C} \) и \(\displaystyle {\rm D} \) по оси \(\displaystyle OX{\small . } \)
Решая это уравнение, получаем:
\(\displaystyle x=-\sqrt{ 11} \) или \(\displaystyle x=\sqrt{ 11}{\small . } \)
Из положения на графике следует, что точка \(\displaystyle {\rm C} \) имеет отрицательную координату по оси \(\displaystyle OX{\small , } \) а точка \(\displaystyle {\rm D} \) – положительную.
Поэтому \(\displaystyle {\rm C}(-\sqrt{ 11};\, 11) \) и \(\displaystyle {\rm D}(\sqrt{ 11};\, 11) {\small .} \) Следовательно, \(\displaystyle {\rm A}(-\sqrt{ 11};0) \) и \(\displaystyle {\rm B}(\sqrt{ 11};0){\small . }\)
Ответ: \(\displaystyle {\rm A}(-\sqrt{ 11};0) \) и \(\displaystyle {\rm B}(\sqrt{ 11};0){\small . }\)
